AT_icpc2014summer_day2_d Dense Amidakuji

有一个阿弥陀籤，它有 $w$ 条高度为 $h$ 的垂直短棒（高度指可以添加水平短棒的段数），其中 $w$ 为偶数。 我们记 $(a, b)$ 表示从上到下第 $a$ 段，从左到右第 $b$ 根垂直短棒上可以添加水平短棒的位置（在 $(a, b)$ 上添加的水平短棒，会在第 $a$ 段连接第 $b$ 根和第 $b + 1$ 根垂直短棒）。可以发现，这样的位置 $(a, b) ~ (1 \le a \le h, 1 \le b \le w - 1)$ 总共有 $h(w - 1)$ 个。 Snuke 君首先在所有满足 $a \equiv b \pmod 2$ 的位置 $(a, b)$ 添加了水平短棒，然后拿走了 $(a_1, b_1), \ldots, (a_n, b_n)$ 位置上的水平短棒。 在这种状态下，请求出对于每个 $i ~ (1 \le i \le w)$，从左边开始的第 $i$ 根垂直短棒顶端出发，到达底端时位于哪根垂直短棒。 注：行走的规则为，在一根垂直短棒上向下走，一旦遇到一根水平短棒，就沿着水平短棒走到其相连的另一根垂直短棒，然后继续向下重复此过程，直到到达底端。

> $h \quad w \quad n$ > $a_i \quad b_1$ > $\cdots$ > $a_n \quad b_n$

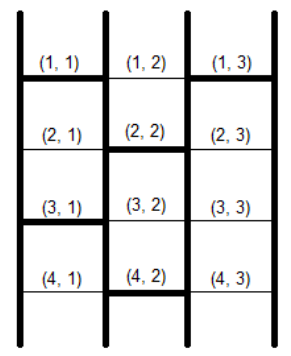
输出 $w$ 行。第 $i$ 行表示，从左边开始的第 $i$ 根垂直短棒顶端出发，到达底端时所在的垂直短棒编号。 ## 输入输出样例 __样例输入 1__ ```plain 4 4 1 3 3 ``` __样例输出 1__ ```plain 2 3 4 1 ``` __样例解释 1__  举例来说，如果选择从最左侧（第 $1$ 根）垂直短棒的顶端出发，会依次经过 $(1, 1)$，$(2, 2)$，$(4, 2)$，最终到达第 $2$ 根垂直短棒的底端。 __样例输入 2__ ```plain 10 6 10 10 4 4 4 5 1 4 2 7 3 1 3 2 4 8 2 7 5 7 1 ``` __样例输出 2__ ```plain 1 4 3 2 5 6 ```

- $1 \le h, w, n \le 200, 000$。 - $w$ 为偶数。 - $1 \le a_i \le h$。 - $1 \le b_i \le w - 1$。 - $a_i \equiv b_i \pmod 2$。 - 不存在 $i, j ~ (i \neq j)$，使得 $(a_i, b_i) = (a_j, b_j)$。