AT_icpc2015summer_day2_d 真っ暗な部屋

[problemUrl]: https://atcoder.jp/contests/jag2015summer-day2/tasks/icpc2015summer_day2_d 入力は以下の形式で標準入力から与えられる。 > $ N $ $ M $ $ K $ $ D_1 $ $ D_2 $ $ ... $ $ D_M $ $ v_{1,1} $ $ v_{1,2} $ $ ... $ $ v_{1,K} $ $ v_{2,1} $ $ v_{2,2} $ $ ... $ $ v_{2,K} $ $ ... $ $ v_{N,1} $ $ v_{N,2} $ $ ... $ $ v_{N,K} $ 答えを一行に出力せよ。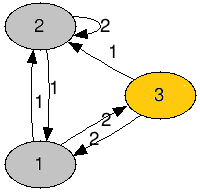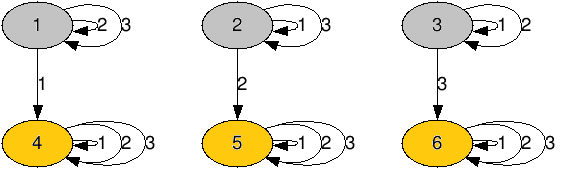 ``` 4 2 2 1 2 2 4 3 1 4 2 1 3 ``` ``` 2 ```  1, 1 という指示を出すと - A君の初期位置が部屋1である場合、2つ目の移動で部屋3に到達する - A君の初期位置が部屋2である場合、1つ目の移動で部屋3に到達する ``` 3 2 2 1 2 2 3 1 2 2 1 ``` ``` 3 ```  2, 1, 2 という指示を出すと - A君の初期位置が部屋1である場合、1つ目の移動で部屋3に到達する - A君の初期位置が部屋2である場合、3つ目の移動で部屋3に到達する ``` 6 3 3 1 2 3 4 1 1 2 5 2 3 3 6 4 4 4 5 5 5 6 6 6 ``` ``` 3 ```  非連結であるケースや、自己辺、多重辺があるケースに気をつけよう

N/A

N/A

### Constraints 目を覚ますと、A君は真っ暗な部屋の中にいた。 どうやらA君は $ N $ 個の部屋から構成されたダンジョンに迷い込んでしまったようだ。 あなたはA君がどの部屋に迷い込んだのかを知ることはできなかったが、幸いにもダンジョンのマップを手に入れることができた。 A君の進むべき道を示し明るい部屋に導こう。 $ N $ 個の部屋のうち $ M $ 個の部屋が真っ暗な部屋であり、それぞれ $ D_1 $, $ D_2 $, $ ... $, $ D_M $ 番目の部屋が真っ暗な部屋であることが分かっている。 また、全ての部屋からちょうど $ K $ 本の一方通行の道が順に並んでおり、$ i $ 番目の部屋から出る道はそれぞれ $ v_{i,1} $, $ v_{i,2} $, ..., $ v_{i,K} $ 番目の部屋に繋がっている。 あなたは、A君に対し今いる部屋から $ a_1 $, $ a_2 $, $ ... $, $ a_l $ 番目の道を順に進ませることができる。 ただし、A君は明るい部屋に到達したらそれ以降の指示は無視する。 あなたは、指示の前後においてA君が今いる部屋の情報を知ることはできないため、A君がどの部屋にいたとしても明るい部屋に辿り着けるような指示列を伝えなければならない。 そのような指示のうち、最も短いものの長さを答えよ。 - - - - - - - $ 2\ \leq\ N\ \leq\ 100 $ - $ 1\ \leq\ M\ \leq\ min(16,\ N-1) $ - $ 1\ \leq\ K\ \leq\ N $ - $ 1\ \leq\ D_i\ \leq\ N $ - $ D_i $ は全て異なる - $ 1\ \leq\ v_{i,\ j}\ \leq\ N $ - 全ての暗い部屋は少なくとも1つの明るい部屋に到達可能である