AT_indeednow_2015_finala_e Page Rank

[problemUrl]: https://atcoder.jp/contests/indeednow-finala-open/tasks/indeednow_2015_finala_e ある会社には $ n $ 人の社員がいる。 この会社では座席が一直線上に並んでおり、この直線の端から順に社員番号が割り当てられている。 この会社では社員の能力を測定するために、以下に述べる方法を使用している。 まず、すべての社員は優秀だと思っている社員のリストを会社に提出する。 $ i $ 番目の社員が提出したリストを $ N(i) $ とする。 遠くの席にいる社員のことはよくわからないので、$ N(i) $ には座席が机 $ 10 $ 個分以上離れている社員が含まれていることはない。 (任意の $ x\ \in\ N(i) $ について $ |i\ -\ x|\ が成り立つ) 全員分のリストを集めたら、社員を頂点とし優秀だと思っている関係を有向辺とするグラフを構築する。 そして、このグラフ上での\ Page\ Rank\ を社員の能力とする。 i $ 番目の社員の Page Rank を $ PR(i) $、$ i $ 番目の社員を優秀だと思っている社員の集合を $ M(i) $ とすると、Page Rank は次の条件式を満たす。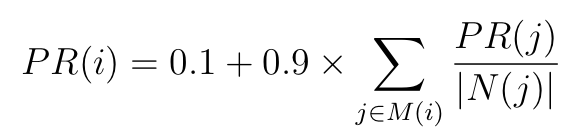  この会社のために Page Rank を求めるプログラムを書くのがあなたの仕事である。

入力は以下の形式で与えられる。 > $ n $ $ m $ $ a_1 $ $ b_1 $ $ ... $ $ a_m $ $ b_m $ - $ 1 $ 行目には社員数を表す整数 $ n $ ($ 1\ \leq\ n\ \leq\ 10{,}000 $)、ある社員が別の社員を優秀だと思っている関係の個数を表す整数 $ m $ ($ 1\ \leq\ m\ \leq\ 10{,}000 $) が与えられる。 - 続く $ m $ 行には、$ 2 $ つの整数 $ a_i $, $ b_i $ ($ 1\ \leq\ a_i,\ b_i\ \leq\ n,\ |a_i\ -\ b_i|\ )\ が含まれており、これは\ a_i $ 番目の社員は $ b $ 番目の社員を優秀だと思っていることを表す。

それぞれの社員に対する Page Rank の値を一行で出力せよ。 相対誤差または絶対誤差が $ 10^{-6} $ 以下ならば正解とみなされる。

### Sample Explanation 2 この場合は $ 3 $ 人の社員がいる。 $ 1 $ 番目の社員は $ 2 $ 番目の社員と $ 3 $ 番目の社員を優秀だと思っている。 $ 2 $ 番目の社員は $ 1 $ 番目の社員を優秀だと思っている。 $ 3 $ 番目の社員は $ 1 $ 番目の社員を優秀だと思っている。 したがって、各社員の Page Rank は以下の条件をすべて満たす。 $ PR(1)\ =\ 0.1\ +\ 0.9\ (\frac{PR(2)}{1}\ +\ \frac{PR(3)}{1}) $ $ PR(2)\ =\ 0.1\ +\ 0.9\ (\frac{PR(1)}{2}) $ $ PR(3)\ =\ 0.1\ +\ 0.9\ (\frac{PR(1)}{2}) $