AT_indeednow_2015_quala_4 パズル

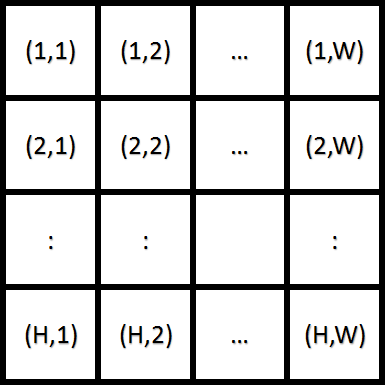
[problemUrl]: https://atcoder.jp/contests/indeednow-quala/tasks/indeednow_2015_quala_4 あなたには、以下のような縦 $ H $マス、横 $ W $ マスのスライドパズルの盤面が与えられます(図1)。  図1. スライドパズル盤面 各マスには、相異なる $ 1 $ から $ H×W-1 $ までの番号が割り振られており、さらにある $ 1 $ つのマスは空きマスとなっています。 このスライドパズルでは、空白マスを左右上下のマスのいずれかと入れ替える操作が許されています。 ただし、入れ替えたい方向にマスが存在しない場合は入れ替えることができません。 この盤面に入れ替え操作を任意の回数行い、完成の状態にしたいと思っています。 ここで、完成の状態とは、左上のマスから順番に番号付けされており右下が空白マスであるような状態にしたいと思っています(図2)。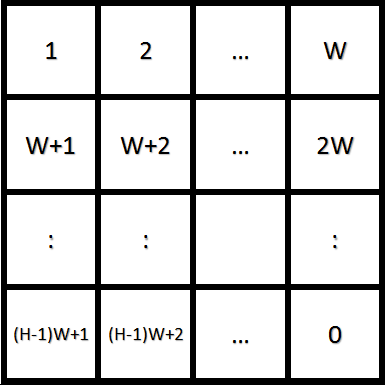  図2. 完成盤面 つまり、完成盤面とは、 - 番号 $ i\ (1≦i≦H×W-1) $ のマスは $ (1+[(i-1)÷W],1+(i-1)%W) $ にある - さらに、空きマスが $ (H,W) $ にある という状態を指します。$ [a÷b] $ は $ a $ を $ b $ で割った値の小数点以下を切り捨てたもの、$ a%b $ は $ a $ を $ b $ で割った余りを指します。 最小操作数が $ 24 $ 回以内ということが保障されているとき、パズルを解くのに必要な最小操作数を出力しなさい。

入力は以下の形式で標準入力から与えられる。 > $ H $ $ W $ $ c_{1,1} $ $ c_{1,2} $ … $ c_{1,W} $ $ c_{2,1} $ $ c_{2,2} $ … $ c_{2,W} $ : $ c_{H,1} $ $ c_{H,2} $ … $ c_{H,W} $ - $ 1 $ 行目には、パズルの盤面の縦方向の長さを表す整数 $ H\ (2≦H≦6) $ と横方向の長さを表す整数 $ W\ (2≦W≦6) $ がスペース区切りで与えられる。 - $ 2 $ 行目から $ H $ 行には、パズルの盤面の情報が与えられる。そのうち $ i\ (1≦i≦H) $ 行目には、スライドパズルの座標 $ (i,1),(i,2),...,(i,W) $ のマスに書かれている数字を表す整数 $ c_{i,1},c_{i,2},...,c_{i,W} $ がスペース区切りで与えられる。ただし、$ c_{i,j}=0 $のときは特別に、そのマスが空マスであることを表す。 - パズルの盤面には、$ 1 $ から $ H×W-1 $ までの整数が1つと、空マスを表す整数 $ 0 $ がちょうど $ 1 $ つずつ現れることが保障されている。 - パズルを解く最小操作数が $ 24 $ 回以内ということが保障されている。

$ 1 $ 行目に、パズルを解く最小操作数を出力せよ。末尾の改行を忘れないこと。

### Sample Explanation 1 最初、空きマスは $ (1,2) $ にあります。この空きマスを「右→下→下」と動かすことで完成の状態にすることができ、そのとき最小操作回数を達成します。 ### Sample Explanation 4 パズルが元から完成している場合もあります。 ### Sample Explanation 5 出力する答えが最大となるケースです。