AT_indeednow_2015_quala_4 パズル

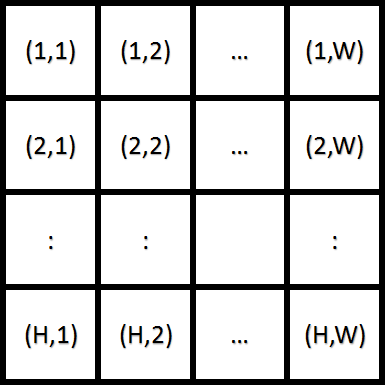
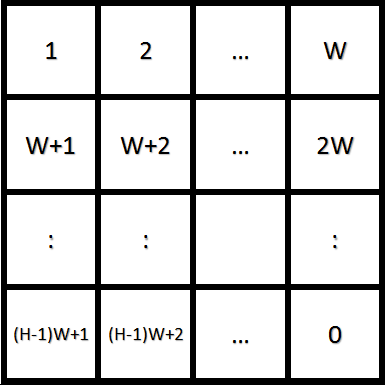
你得到了一个如下所示的纵向 $H$ 格、横向 $W$ 格的滑块拼图棋盘（见图1）。  图1. 滑块拼图棋盘 每个格子上都标有互不相同的 $1$ 到 $H \times W-1$ 的编号，另外有一个格子为空格。 在这个滑块拼图中，允许你将空格与其上下左右相邻的格子交换。若所选方向上没有格子，则无法交换。 你可以任意次进行上述交换操作，目标是将棋盘变为完成状态。完成状态指的是：从左上角开始按顺序编号，右下角为空格的状态（见图2）。  图2. 完成棋盘 具体来说，完成棋盘满足以下条件： - 编号为 $i\ (1 \leq i \leq H \times W-1)$ 的格子在 $(1+[(i-1) \div W], 1+(i-1)\%W)$ 处； - 空格在 $(H, W)$ 处。 这里，$[a \div b]$ 表示将 $a$ 除以 $b$ 后向下取整的结果，$a\%b$ 表示 $a$ 除以 $b$ 的余数。 已知最小操作次数不会超过 $24$，请输出解开该拼图所需的最小操作次数。

输入通过标准输入给出，格式如下： > $H$ $W$ $c_{1,1}$ $c_{1,2}$ … $c_{1,W}$ > $c_{2,1}$ $c_{2,2}$ … $c_{2,W}$ > … > $c_{H,1}$ $c_{H,2}$ … $c_{H,W}$ - 第 $1$ 行给出棋盘的纵向长度 $H\ (2 \leq H \leq 6)$ 和横向长度 $W\ (2 \leq W \leq 6)$，以空格分隔。 - 接下来 $H$ 行，每行 $W$ 个整数，表示滑块拼图的棋盘信息。第 $i$ 行的 $c_{i,1}, c_{i,2}, ..., c_{i,W}$ 依次表示第 $i$ 行第 $1$ 列到第 $W$ 列的格子上的数字。若 $c_{i,j}=0$，表示该格为空格。 - 棋盘上恰好出现 $1$ 到 $H \times W-1$ 的整数各一次，以及一个空格（$0$）。 - 保证解开拼图的最小操作次数不超过 $24$。

输出一行，表示解开拼图所需的最小操作次数。不要忘记输出末尾的换行符。

### 样例解释 1 初始时，空格在 $(1,2)$。将空格依次向「右→下→下」移动即可完成拼图，此时操作次数最少。 ### 样例解释 4 也有可能棋盘一开始就是完成状态。 ### 样例解释 5 这是需要输出最大操作次数的情况。 由 ChatGPT 4.1 翻译