AT_indeednow_2015_qualc_3 木

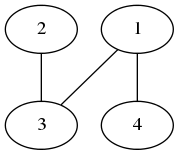
树是一种由顶点和连接这些顶点的边组成的结构“图”的一种特殊形式。若顶点数为 $N$，则边的数量为 $N-1$，并且任意两个顶点都通过边直接或间接相连。  本题中，树有 $N$ 个顶点，编号从 $1$ 到 $N$。 给定一棵树，请输出通过以下操作得到的字典序最小的数列： 1. 选择顶点 $1$。 2. 重复以下操作，直到没有未被选择的顶点为止：从所有与已选择顶点通过边直接相连、且尚未被选择的顶点中，选择编号最小的一个顶点。 3. 按照顶点被选择的顺序，构成一个数列。 对于长度为 $N$ 的序列 $A=\{a_1,a_2,\ldots,a_N\}$ 和 $B=\{b_1,b_2,\ldots,b_N\}$，若存在 $k(1\leq k\leq N)$ 使得对于所有 $i

输入按以下格式从标准输入读入。 > $N$ > $a_1$ $b_1$ > $a_2$ $b_2$ > $\vdots$ > $a_{N-1}$ $b_{N-1}$ - 第 $1$ 行为一个整数 $N\ (2\leq N\leq 10^5)$，表示树的顶点数。 - 接下来的 $N-1$ 行，每行包含两个整数 $a_i$、$b_i$，表示顶点 $a_i$ 和顶点 $b_i$ 之间有一条边。 - 保证输入的 $N$ 个顶点和 $N-1$ 条边构成一棵树。

请输出通过上述操作得到的字典序最小的数列，数之间用空格分隔。 注意行末需要换行，且行末不能有多余的空格。

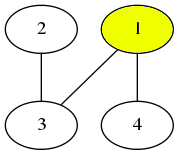
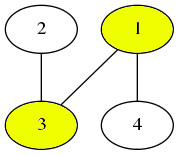
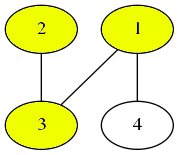
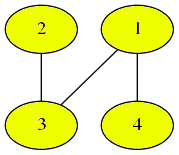
### 部分分 本题设置了部分分。 - 有 $50$ 分的测试点满足 $1\leq N\leq 3,000$。 ### 样例解释 1 这是题目描述中的树。首先，选择顶点 $1$。  接下来，选择顶点 $3$。注意，顶点 $2$ 与已选择的顶点（此时仅有顶点 $1$）没有边直接相连，因此不能被选择。  然后，选择顶点 $2$。  接着，选择顶点 $4$。  按选择顺序排列顶点编号，得到 $1\ 3\ 2\ 4$。不存在比这个序列字典序更小的选择方式。 由 ChatGPT 4.1 翻译