AT_jag2016secretspring_d インビジブル
题目描述
你和朋友正准备玩一款名为「インビジブル(Invisible)」的卡牌游戏。在这款游戏中使用两种卡牌:“得分卡”和“妨碍卡”。每张得分卡上都标有一个正数值。该卡牌游戏的规则如下:
- 游戏由玩家 1 和玩家 2 两位玩家进行,游戏从玩家 1 的回合开始。
- 场上有一个堆叠区和两副牌。堆叠区由两位玩家放置的卡片组成;每位玩家的牌库则由该玩家持有的所有得分卡和妨碍卡构成。玩家可以随时查看自己或对手牌库中卡片的顺序。游戏开始时,堆叠区中没有任何卡片。
- 两名玩家交替进行以下两种行动中的一种,每个回合恰好执行一次:
- 将自己牌库顶端的卡片放到堆叠区的最上方。但当自己牌库中没有任何卡片时,无法执行此行动。
- 跳过自己的回合。
- 当某名玩家选择跳过回合时,进行以下处理:
- 每位玩家获得堆叠区中所有满足下列两个条件的得分卡,获得的得分卡从场上移除:
1. 该得分卡是自己放到堆叠区里的。
2. 它在堆叠区中位于对手所放置的任何妨碍卡之上。(如果堆叠区中不存在对手放的妨碍卡,该玩家就获得自己放到堆叠区里的所有卡。)
- 然后清空堆叠区中的所有卡。
如果在堆叠区中没有任何卡片且双方玩家连续跳过回合,则游戏结束。每位玩家的最终得分为其所获得的所有得分卡上所标数值之和。
每位玩家都会采取最优行动以最大化自己得分减去对手得分的差值;你的任务是:对于给定的两位玩家的牌库,在双方均按最优策略行事时,计算玩家 1 与玩家 2 得分之差。
输入格式
输入由单组数据构成,格式如下。
> $n \ \ m$
> $a _ 1 \ \ a _ 2 \ \ \cdots \ \ a _ n$
> $b _ 1 \ \ b _ 2 \ \ \cdots \ \ b _ n$
第一行是两个正整数 $n, m$($1 \le n, m \le 50$),分别表示玩家 1 和玩家 2 牌库中的卡牌数。第二行包含 $n$ 个整数 $a _ 1, a _ 2, \cdots , a _ n$,$a _ i$ 表示玩家 1 牌库中从上到下第 $i$ 张卡的类型($1 \le i \le n$)。若 $a _ i$ 为 $1$ 至 $1{,}000{,}000$ 的正整数,则表示一张得分卡,其点数即该值;若 $a _ i$ 为 $−1$,则表示一张妨碍卡。第三行包含 $m$ 个整数 $b _ 1, b _ 2, \cdots, b _ m$,$b _ j$ 表示玩家 2 牌库中从上到下第 $j$ 张卡的类型($1 \le j \le m$)。若 $b _ j$ 为 $1$ 至 $1{,}000{,}000$ 的正整数,则表示一张得分卡,其点数即该值;若 $b _ j$ 为 $−1$,则表示一张妨碍卡。
输出格式
在双方玩家都采取最优行动时,输出玩家 1 的得分减玩家 2 的得分。
说明/提示
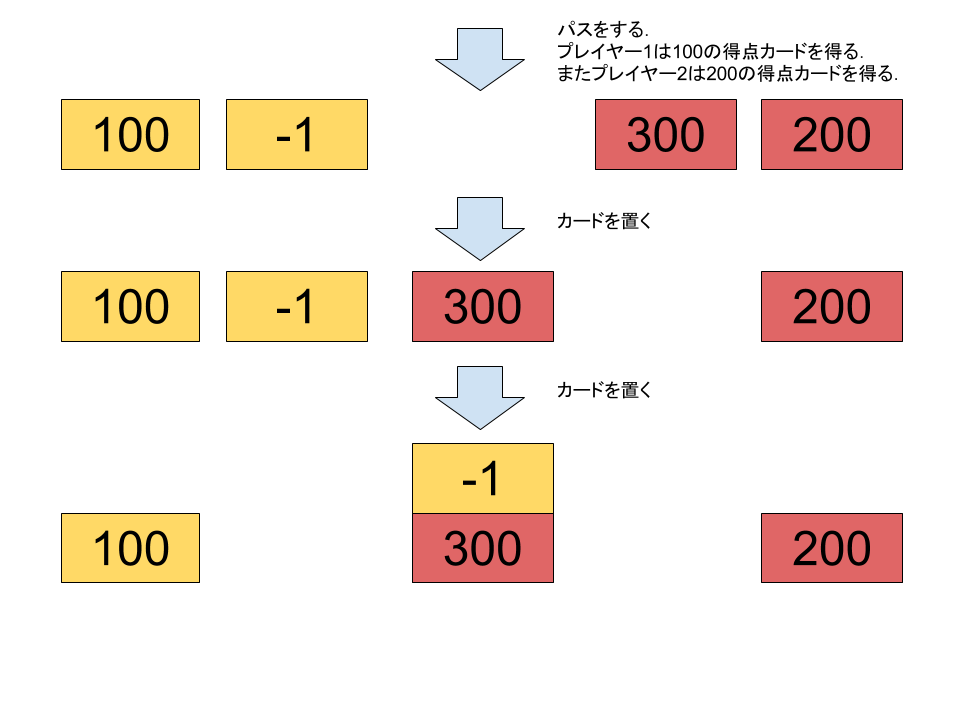
### 样例解释 \#1