AT_jag2017summer_day1_d くさかべ

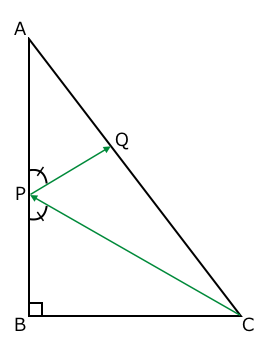
[problemUrl]: https://atcoder.jp/contests/jag2017summer-day1/tasks/jag2017summer_day1_d 日下部さんは壁に反射するのが大好きで、今日も元気に壁に反射して遊んでいます。 今日の壁は、直角三角形の部屋の壁です。 下図のように三角形の頂点をそれぞれ $ A,B,C $ と呼ぶことにします。 日下部さんは頂点 $ C $ から点 $ P $ に向かってまっすぐ歩き、点 $ P $ に着くと、角 $ BPC $ = 角 $ APQ $ となるような辺 $ AC $ 上の点 $ Q $ に向かって再びまっすぐ歩きました。  線分 $ AB $ の長さは $ X $、線分 $ BC $ の長さは $ Y $、線分 $ AQ $ の長さは $ Z $ でした。 このとき、線分 $ AP $ の長さはいくらでしょうか？

入力は以下の形式で標準入力から与えられる。 > $ X $ $ Y $ $ Z $

線分 $ AP $ の長さを出力せよ。 ただし、絶対誤差または相対誤差が $ 10^{-9} $ 以下ならば正解とみなされる。

### 制約 - $ 1≦X,Y≦100 $ - $ 1≦Z\