AT_joi2006yo_d JOI 2006 予選 問題4

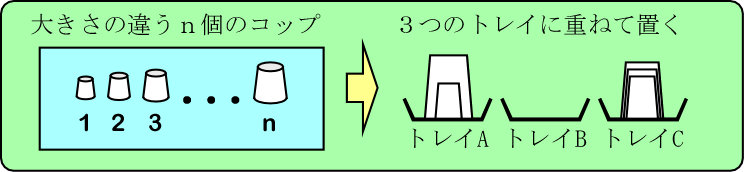
[problemUrl]: https://atcoder.jp/contests/joi2006yo/tasks/joi2006yo_d 大きさが異なる $ n $ 個のコップと $ 3 $ つのトレイ（お盆）A，B，C があり，それらのコップは $ 3 $ つのトレイの上にそれぞれ何個かずつ一山に重ねて置かれている．ただし，どのトレイにおいても，そのトレイの中で一番小さいコップが一番下に，$ 2 $ 番目に小さいコップがその上に，$ 3 $ 番目に小さいコップがその上にと，小さい順に伏せて重ねてある．例えば，下図の右側は，$ n\ =\ 5 $ 個のコップがトレイ A，B，C にそれぞれ $ 2 $ 個，$ 0 $ 個，$ 3 $ 個重ねて置かれている状態を示している．  このように，コップの初期状態が与えられたとき，次の規則 $ 1 $ ～ $ 3 $ を守りながら，すべてのコップを A または C のどちらかのトレイに移動させるには何回移動を行えばよいかを求めたい． （規則 $ 1 $） $ 1 $ 回に $ 1 $ つのコップだけを移動させることができる．それは，そのトレイにあるコップの中で一番上のコップ （つまり，一番大きいコップ）である． （規則 $ 2 $） 大きいコップの上に小さいコップを重ねてはいけない． （規則 $ 3 $） コップ $ 1 $ 個の直接移動は，トレイ A から B，B から A，B から C，C から B のみが許され，A から C への直接移動や C から A への直接移動は許されない． $ n $ 個のコップの初期状態と整数 $ m $ が与えられたとき，$ m $ 回以内の移動で，A または C のどちらかのトレイにすべてのコップをまとめて重ねることができるかどうかを判定し，可能な場合には移動回数の最小値を，不可能な場合には $ -1 $ を出力するプログラムを作成しなさい． 入力の $ 1 $ 行目には，$ n $ と $ m $ がこの順に空白を区切り文字として書いてある．$ 1\ \leqq\ n\ \leqq\ 15 $ であり，$ 1\ \leqq\ m\ \leqq\ 15\,000\,000 $ である．$ 2 $ 行目，$ 3 $ 行目，$ 4 $ 行目には，$ 1 $ から $ n $ までの整数を何個かずつ $ 3 $ つのグループに分けて，それぞれのグループ内で小さい順（昇順）に並べたものが書いてある．ただし，各行の先頭（それらの整数の前）には，それらの個数が書いてある．$ 2 $ 行目に書かれている整数（先頭の $ 1 $ つを除く）はトレイ A の上に重ねられている各コップの大きさを表す．同様に，$ 3 $ 行目に書かれている整数（先頭の $ 1 $ つを除く）はトレイ B の上に重ねられている各コップの大きさを表し，$ 4 $ 行目に書かれている整数（先頭の $ 1 $ つを除く）はトレイ C の上に重ねられている各コップの大きさを表す． 出力においては，出力（移動回数または $ -1 $）の後に改行を入れること． - - - - - -

N/A

N/A

### Sample Explanation 1 \- - - - - - ### Sample Explanation 2 \- - - - - - ### Sample Explanation 3 \- - - - - -