AT_joi2006yo_d JOI 2006 予選 問題4

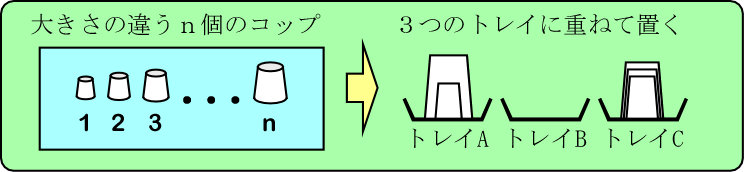
现有大小各异的 $ n $ 个杯子以及 $ 3 $ 个托盘 A、B 和 C。其中，这些杯子已经根据大小分别倒扣在这 $ 3 $ 个托盘上。在每个托盘上，杯子按照从小到大的顺序堆叠（即最小的在最底下，第二小的在上面，依此类推）。例如，下图右侧展示了当 $ n = 5 $ 时，托盘 A 上有 $ 2 $ 个杯子，托盘 B 上没有杯子，托盘 C 上有 $ 3 $ 个杯子的情况。  在保证遵循下述规则 1 到 3 的前提下，我们需要将所有杯子移到托盘 A 或托盘 C 上，并计算所需的最少移动次数。 1. 每次只能移动一个杯子，并且只能是该托盘顶部的杯子（即最大号的）。 2. 小号的杯子不能放在大号杯子之上。 3. 杯子的直接移动仅限于托盘 A 到 B，B 到 A，B 到 C 和 C 到 B，不允许直接从 A 移动到 C 或从 C 移动到 A。 给定杯子初始状态以及一个整数 $ m$，要求你判断是否能在最多 $ m $ 次移动内，将所有杯子移到托盘 A 或 C 上。如果可能，输出所需的最少移动次数；如果不可能，输出 $ -1 $。 输入的第一行为两个整数 $ n $ 和 $ m $（以空格分隔），分别表示杯子数量和允许的最多移动次数。接下来的三行每行以一个整数开头，表示该行中紧接着几个整数的数量。后续的整数表示托盘 A、B 和 C 上的杯子大小，已按升序排列。 输出一个整数，表示最少的移动次数或 $ -1 $，并在输出后换行。

第一行：两个整数 $ n $ 和 $ m $（1 ≤ $ n $ ≤ 15，1 ≤ $ m $ ≤ 15,000,000） 接下来三行：每行第一个整数表示后续杯子的数量，后续整数表示该托盘上的杯子大小，按升序排列。

输出一个整数，表示最少的移动次数或 $ -1 $，并在输出后换行。 **本翻译由 AI 自动生成**

### Sample Explanation 1 \- - - - - - ### Sample Explanation 2 \- - - - - - ### Sample Explanation 3 \- - - - - -