AT_joi2006yo_e JOI 2006 予選 問題5

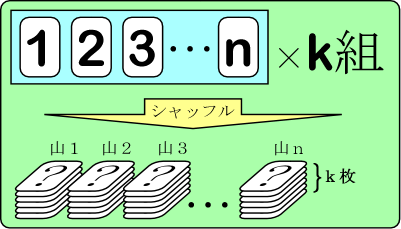
[problemUrl]: https://atcoder.jp/contests/joi2006yo/tasks/joi2006yo_e 次のようなゲームを考える．$ 1 $ から $ n $ までの数が $ 1 $ つずつ書かれた $ n $ 枚のカードが $ k $ 組ある．これら $ kn $ 枚のカードをよくシャッフル（よく切ること）して，$ k $ 枚ずつの山を作り横一列に並べる．このようにしてできる $ n $ 個の山の左から $ i $ 番目の（$ k $ 枚のカードの）山を「山 $ i $」と呼ぶことにする．  ゲームは山 $ 1 $ から始める．山の一番上のカード $ 1 $ 枚を引き（引いたカードは元の山に戻さない），そのカードに書かれていた数が $ i $ だった場合には山 $ i $ の一番上のカード $ 1 $ 枚を引く．このようにして，引いたカードに書かれていた数を番号とする山の一番上のカード $ 1 $ 枚を引くことを繰り返し，すべての山にカードが無くなれば成功である．まだカードが残っている山があるのに，次にカードを引くべき山が無くなっていた場合は失敗である． 途中で失敗した場合には，そのまま失敗で終了するか，または残ったカードの山をそのまま（山の番号もそのまま）にしてゲームを再開する．ゲームを再開する場合は，最初に引くカードはカードが残っている山のうちの一番左の山からとする（その山の一番上のカードが最初に引かれるカードとなる）．再開後も再開前と同様の方法でゲームを進め，すべての山にカードが無くなれば成功であり，まだカードが残っている山があるのに，次にカードを引くべき山が無くなった場合は失敗である．  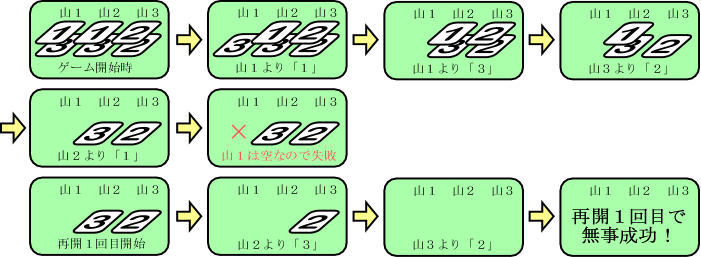このようなゲームの再開を最大 $ m $ 回まで行うものとする．ただし，$ m $ は $ 0 $ か $ 1 $ である．つまり，$ 1 $ 回も再開しないか，$ 1 $ 回だけ再開するかのいずれかである．ゲーム開始前のシャッフルの仕方によりカードの初期配置は異なる．当然，カードの初期配置により，再開せずに成功することもあれば，再開して成功することも，再開して失敗することもある．十分シャッフルしているので，どの初期配置も全て同じ確率で現れるものと考えることにして，再開が $ m $ 回以内で成功する確率 $ p $ を求めたい．この確率 $ p $ を小数で表し，小数第 $ r $ 位まで求めて出力するプログラムを作りなさい．ただし，次の条件を満たすように出力すること． 十分大きい正整数 $ K $ を取ると $ p\ \times\ 10^K $ が 整数となる場合，小数部は途中から $ 0 $ が続くが，その $ 0 $ も出力すること．例えば，$ p\ =\ 3/8\ =\ 0.375 $ の場合，$ r\ =\ 5 $ なら $ 0.37500 $ と出力し，$ r\ =\ 2 $ なら $ 0.37 $ と出力する．$ p\ =\ 1.0 $ の場合も同様に，例えば $ r\ =\ 3 $ なら $ 1.000 $ と出力すること． 例えば $ 0.150000\cdots $ は循環小数 $ 0.1499999\cdots $ として表すこともできるが，このような場合，前者の表し方を用いる． 入力の $ 1 $ 行目には整数 $ n,\ k,\ m,\ r $ がこの順に空白を区切り文字として書いてある．$ 1\ \leqq\ n\ \leqq\ 10\,000 $，$ 1\ \leqq\ k\ \leqq\ 100 $，$ m\ =\ 0 $ または $ m\ =\ 1 $，$ 1\ \leqq\ r\ \leqq\ 10\,000 $ である． 出力においては，指定通りに出力した $ p $ の後に改行を入れること． - - - - - -

N/A

N/A

### Sample Explanation 1 \- - - - - - ### Sample Explanation 2 \- - - - - -