AT_joi2009ho_b ピザ

[problemUrl]: https://atcoder.jp/contests/joi2009ho/tasks/joi2009ho_b JOI ピザでは，市の中心部を通る全長 $ d $ メートルの環状線の沿線上でピザの宅配販売を行っている． JOI ピザは，環状線上に $ n $ 個の店舗 $ S_1,\ \ldots,\ S_n $ を持つ．本店は $ S_1 $ である．$ S_1 $ から $ S_i $ まで，時計回りに環状線を移動したときの道のりを $ d_i $ メートルとおく．$ d_2,\ \ldots,\ d_n $ は $ 1 $ 以上 $ d\ -\ 1 $ 以下の整数である．$ d_2,\ \ldots,\ d_n $ は全て異なる． ピザの注文を受けると，ピザが冷めないように，宅配先までの移動距離がもっとも短い店舗でピザを焼き宅配する． 宅配先の位置は $ 0 $ 以上 $ d\ -\ 1 $ 以下の整数 $ k $ で表される．これは，本店 $ S_1 $ から宅配先までに時計回りで環状線を移動したときの道のりが $ k $ メートルであることを意味する．ピザの宅配は環状線に沿って行われ，それ以外の道を通ることは許されない．ただし，環状線上は時計回りに移動しても反時計回りに移動してもよい． 例えば，店舗の位置と宅配先の位置が下図のようになっている場合 (この例は「入出力の例」の例 $ 1 $ と対応している)．  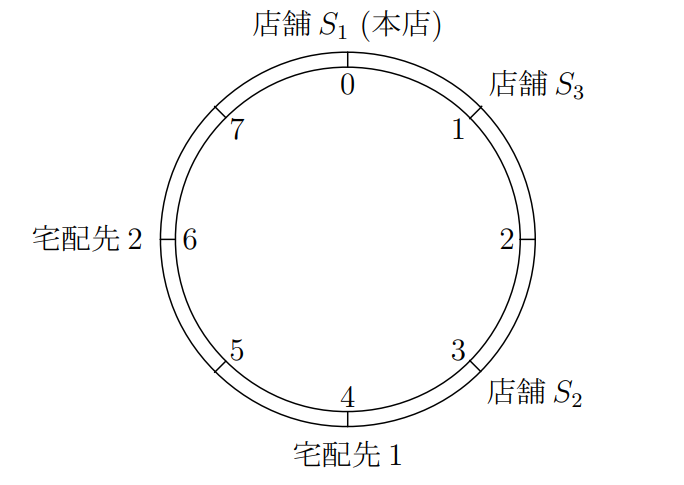宅配先 $ 1 $ にもっとも近い店舗は $ S_2 $ なので，店舗 $ S_2 $ から宅配する．このとき，店舗からの移動距離は $ 1 $ である．また，宅配先 $ 2 $ にもっとも近い店舗は $ S_1 $ (本店) なので，店舗 $ S_1 $ (本店) から宅配する．このとき，店舗からの移動距離は $ 2 $ である． 環状線の全長 $ d $，JOI ピザの店舗の個数 $ n $，注文の個数 $ m $，本店以外の位置を表す $ n\ -\ 1 $ 個の整数 $ d_2,\ \ldots,\ d_n $，宅配先の場所を表す整数 $ k_1,\ \ldots,\ k_m $ が与えられたとき，各注文に対する宅配時の移動距離 (すなわち，最寄店舗から宅配先までの道のり) の全注文にわたる総和を求めるプログラムを作成せよ． - - - - - -

$ 1 $ 行目には環状線の全長を表す正整数 $ d $ ($ 2\ \leqq\ d\ \leqq\ 1\,000\,000\,000\ =\ 10^9 $)，$ 2 $ 行目には店舗の個数を表す正整数 $ n $ ($ 2\ \leqq\ n\ \leqq\ 100\,000 $)，$ 3 $ 行目には注文の個数を表す正整数 $ m $ ($ 1\ \leqq\ m\ \leqq\ 10\,000 $) が書かれている．$ 4 $ 行目以降の $ n\ -\ 1 $ 行には本店以外の店舗の位置を表す整数 $ d_2,\ d_3,\ \ldots,\ d_n $ ($ 1\ \leqq\ d_i\ \leqq\ d\ -\ 1 $) がこの順に書かれており，$ n\ +\ 3 $ 行目以降の $ m $ 行には宅配先の場所を表す整数 $ k_1,\ k_2,\ \ldots,\ k_m $ ($ 0\ \leqq\ k_i\ \leqq\ d\ -\ 1 $) がこの順に書かれている． 採点用データのうち，配点の $ 40 $ %分については，$ n\ \leqq\ 10\,000 $ を満たす．また，配点の $ 40 $ %分については，求める移動距離の総和と $ d $ の値はともに $ 1\,000\,000 $ 以下である．さらに，全ての採点用データにおいて，求める移動距離の総和は $ 1\,000\,000\,000\ =\ 10^9 $ 以下である．

出力は，宅配時の移動距離の総和を表す $ 1 $ つの整数のみを含む $ 1 $ 行からなる． - - - - - -

### Sample Explanation 1 \- - - - - -