AT_joi2009yo_c 連鎖

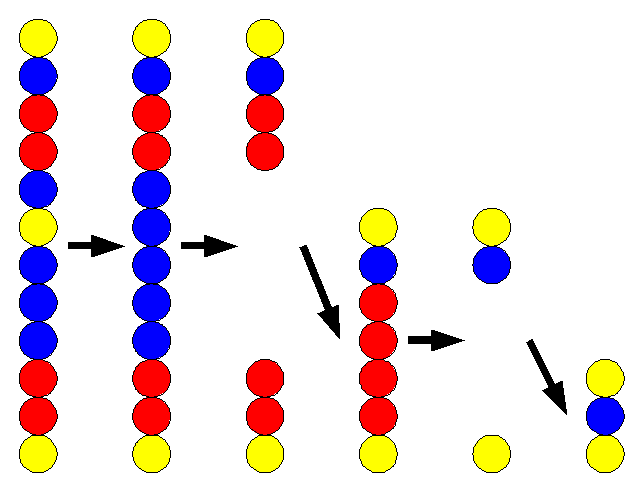
有如下的一个游戏。 有 $N$ 个角色竖直排列成 $1$ 列。这些角色的颜色可以是红色、蓝色或黄色，初始状态下不会有 $4$ 个及以上相同颜色的角色连续排列。玩家可以选择某个位置的角色，将其颜色更改为其他颜色。如果通过这次操作后，出现了 $4$ 个及以上相同颜色的角色连续排列，那么这些角色会被消除。由于角色被消除，可能会再次出现 $4$ 个及以上相同颜色的角色连续排列，这些角色也会被消除。这个连锁反应会一直持续，直到没有 $4$ 个及以上相同颜色的角色连续排列为止。游戏的目标是让最终未被消除的角色数尽可能少。 例如，下图左侧的初始状态下，将从上往下第 $6$ 个角色的颜色从黄色改为蓝色后，会出现 $5$ 个连续的蓝色角色被消除，最终只剩下 $3$ 个角色未被消除。  给定初始状态下 $N$ 个角色的颜色排列，请编写程序，求只更改一个角色颜色后，最终未被消除的角色数的最小值 $M$。

第 $1$ 行为角色数 $N$，满足 $1 \leq N \leq 10\,000$。接下来的 $N$ 行，每行包含一个整数 $1$、$2$ 或 $3$，表示初始状态下从上往下第 $i$ 个角色的颜色（$1$ 表示红色，$2$ 表示蓝色，$3$ 表示黄色）。

输出只更改一个角色颜色后，最终未被消除的角色数的最小值 $M$。

### 样例解释 1 —— 由 ChatGPT 4.1 翻译