AT_joi2009yo_f ビンゴ

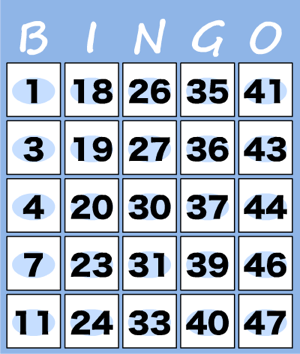
在某次编程竞赛之后，传统上会进行一个特殊的宾果游戏。用来玩的宾果卡片有如下的制作规则： - 宾果卡片是 $N$ 行 $N$ 列的网格，每个格子里都有一个唯一的正整数。 - 每个格子中的数值范围在 $1$ 到 $M$ 之间。 - 整个卡片上 $N \times N$ 个格子的数值之和为 $S$。 - 每一列从上到下排列时，数值按照升序顺序。 - 每个格子中的数值都大于它左侧所有列中的任意一个数值。 以下展示了当 $N = 5$，$M = 50$ 和 $S = 685$ 时的一张符合条件的宾果卡片示例：  为了这次联谊活动，我们想要尽可能地制作更多这样的宾果卡片，但不能制作重复的卡片。请帮助编写一个程序，计算出可以制作的最大宾果卡片数量，并输出这个数量除以 $100\,000$ 的余数。

输入只有一行，由三个用空格分隔的正整数 $N$、$M$ 和 $S$ 组成，分别表示宾果卡片的规模、卡片上数字的最大值和所有数字的总和（$1 \leq N \leq 7$，$1 \leq M \leq 2\,000$，$1 \leq S \leq 3\,000$）。输入保证至少存在一种符合条件的宾果卡片。

输出为能够制作的符合条件的宾果卡片数量对 $100\,000$ 取模之后的结果。 **本翻译由 AI 自动生成**

### Sample Explanation 1 \- - - - - - ### Sample Explanation 2 \- - - - - - ### Sample Explanation 3 入力例 $ 3 $ に対して，作ることができるビンゴカードの枚数の最大値は $ 642\,499\,974\,501 $ であるので，$ 100\,000 $ で割った余りの $ 74\,501 $ を出力する．