AT_joi2014yo_c 超都観光 (Super Metropolis)

# 超都观光 (Super Metropolis) JOI君计划在IOI国的一个名为超都的城市进行观光旅游。 超都被南北方向的 $ W $ 条直线和东西方向的 $ H $ 条直线划分成棋盘状。 南北方向的 $ W $ 条直线从西向东依次编号为 $ 1,\ 2,\ \ldots,\ W $。东西方向的H条直线从南向北依次编号为 $ 1,\ 2,\ \ldots,\ H $。将从西向东第 $ i $ 条南北向的直线和从南向北第 $ j $ 条东西向的直线的交叉点记作 $ (i,\ j) $ 。 此外，每个交叉点都有一条通往东北方向交叉点的路（除了最北边和最东边的直线上的交叉点），以及一条通往西南方向交叉点的路（除了最南边和最西边的直线上的交叉点）。也就是说，从交叉点 $ (i,\ j) $ 出发，如果存在交叉点 $ (i\ -\ 1,\ j) $, $ (i\ +\ 1,\ j) $, $ (i,\ j\ -\ 1) $, $ (i,\ j\ +\ 1) $ ，则可以通过一条道路到达这些交叉点。同样，如果存在交叉点 $ (i\ -\ 1,\ j\ -\ 1) $, $ (i\ +\ 1,\ j\ +\ 1) $ ，也可以通过一条道路到达这些交叉点。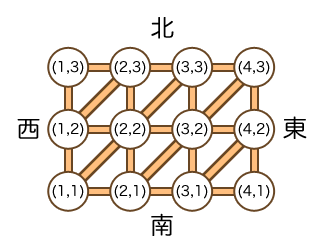  JOI君已经计划好了 $ N $ 个观光景点的访问顺序。第$ i $ 个 $ (1\ \leqq\ i\ \leqq\ N) $ 要访问的景点位于交叉点 $ (X_i,\ Y_i) $ 。JOI君希望尽量减少必须经过的道路数量，以缩短旅行时间。请编写一个程序来计算按照预定顺序访问所有景点至少需要经过的道路总数。 注意，旅行的起点是交叉点 $ (X_1,\ Y_1) $ 。在旅行过程中，不能离开超都。JOI君也可以在不访问景点的情况下通过景点所在的交叉点。 **（预选赛结束后补充）** 关于“道路总数”的补充说明：在旅行过程中，同一条路可以走两次以上。在这种情况下，道路总数将计算走过该路的次数。 by @[Justskr](https://www.luogu.com.cn/user/772284)

输入包含 $ 1\ +\ N $ 行。 第一行包含三个用空格分隔的整数 $ W,\ H,\ N $ ($ 2\ \leqq\ W\ \leqq\ 10\,000 $，$ 2\ \leqq\ H\ \leqq\ 10\,000 $，$ 1\ \leqq\ N\ \leqq\ 1\,000 $) 。 接下来的 $ N $ 行中，第 $ i $ 行包含两个用空格分隔的整数 $ X_i,\ Y_i $ ($ 1\ \leqq\ X_i\ \leqq\ W $，$ 1\ \leqq\ Y_i\ \leqq\ H $) ，表示第 $ i $ 个要访问的景点所在的交叉点。

输出一行，表示按照顺序访问所有景点至少需要经过的道路总数。

### 样例解释 1 在样例 $ 1 $ 中，可以按照 $ (1,\ 1) $, $ (2,\ 2) $, $ (3,\ 3) $, $ (3,\ 2) $, $ (4,\ 2) $, $ (4,\ 1) $ 的顺序访问交叉点。 ### 样例解释 2 在样例 $ 2 $ 中，可能会多次访问同一个交叉点。