AT_joi2023_yo2_c 塗りつぶし (Painting)
题目描述
JOI 君正在用绘图软件涂鸦。
在该绘图软件中,可以在一个高为 $H$ 行、宽为 $W$ 列的矩形格子上绘画。每个格子都有一种颜色,颜色用 $1$ 到 $10^9$ 之间的整数表示。
自上而下的第 $i$ 行($1 \leq i \leq H$),自左而右的第 $j$ 列($1 \leq j \leq W$)的格子记为 $(i,j)$。当前,格子 $(i,j)$ 的颜色为 $A_{i,j}$。
不断从格子 $(i,j)$ 向与其边相邻的格子移动,且只经过与格子 $(i,j)$ 颜色相同的格子,这样能够到达的所有格子的集合,称为“格子 $(i,j)$ 的区域”。
绘图软件有一个名为“填充”的功能。指定一个格子 $(x,y)$($1 \leq x \leq H$,$1 \leq y \leq W$)以及颜色 $c$($1 \leq c \leq 10^9$)后,将格子 $(x,y)$ 的区域内所有格子的颜色都变为 $c$。
JOI 君会选择某个格子 $(x,y)$ 和颜色 $c$,仅进行一次填充操作。填充后,格子 $(x,y)$ 的区域内包含的格子数量作为 JOI 君的得分。
请你求出 JOI 君可以获得的最大得分。
输入格式
输入的格式如下:
> $H$ $W$
> $A_{1,1}$ $A_{1,2}$ $\cdots$ $A_{1,W}$
> $A_{2,1}$ $A_{2,2}$ $\cdots$ $A_{2,W}$
> $\vdots$
> $A_{H,1}$ $A_{H,2}$ $\cdots$ $A_{H,W}$
输出格式
请输出 JOI 君可以达到的最大得分。
说明/提示
## 小子任务
1.(9 分)$H=1$。
2.(32 分)$H \leq 30$,$W \leq 30$,$A_{i,j} \leq 5$($1 \leq i \leq H$,$1 \leq j \leq W$)。
3.(18 分)$H \leq 30$,$W \leq 30$。
4.(10 分)$A_{i,j} \leq 2$($1 \leq i \leq H$,$1 \leq j \leq W$)。
5.(31 分)无其他额外限制。
## 样例解释 1
在初始状态下,格子 $(2,2)$ 的区域包含 $(1,2), (2,1), (2,2), (3,2)$ 共 $4$ 个格子。因此,选择格子 $(2,2)$ 并指定颜色 $3$ 进行填充后,如下图所示,这 $4$ 个格子的颜色都会变为 $3$。
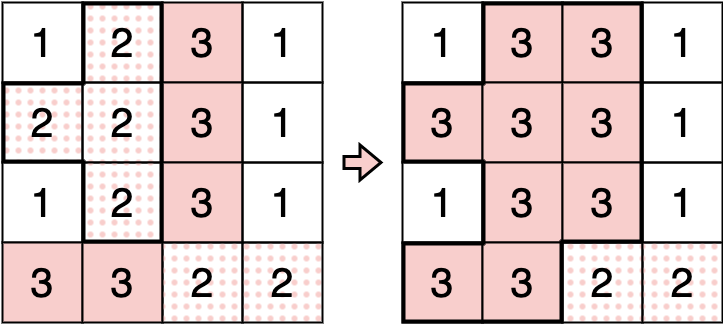
填充后,格子 $(2,2)$ 的区域包含 $(1,2), (1,3), (2,1), (2,2), (2,3), (3,2), (3,3), (4,1), (4,2)$ 共 $9$ 个格子。因此,JOI 君的得分为 $9$。
无法使 JOI 君的得分达到 $10$ 或更大,故输出 $9$。
该输入满足小子任务 $2, 3, 5$ 的限制。
## 样例解释 2
该输入满足小子任务 $2, 3, 5$ 的限制。
## 样例解释 3
该输入满足小子任务 $2, 3, 4, 5$ 的限制。
## 约束条件
- $1 \leq H \leq 500$。
- $1 \leq W \leq 500$。
- $1 \leq A_{i,j} \leq 10^9$($1 \leq i \leq H$,$1 \leq j \leq W$)。
- 输入数据均为整数。
由 ChatGPT 5 翻译