AT_joi2024_yo2_d 庭園 2 (Garden 2)

JOI 庭園は縦 $ N $ 行，横 $ N $ 列のマス目状に区切られた正方形の形をしている． 上から $ i $ 行目 ( $ 1 \leqq i \leqq N $ )，左から $ j $ 列目 ( $ 1 \leqq j \leqq N $ ) のマスは区画 $ (i, j) $ と呼ばれている． JOI 庭園は土壌にあまり恵まれていないため，各区画には特定の $ 1 $ 種類の色の花を，**最大** $ 1 $ 本しか植えることができない． 具体的には，区画 $ (i, j) $ には $ A_{i, j} = $ `R` のとき赤， $ A_{i, j} = $ `Y` のとき黄， $ A_{i, j} = $ `B` のとき青の色の花を最大 $ 1 $ 本しか植えることができない． ここで，この庭園の管理者である K 理事長は，航空写真を撮った時の見栄えを良くするため，次の手順で花を植えようと思っている． 1. **大きさ**を表す整数 $ r $ を決める．ただし $ 0 \leqq r \leqq \frac{N-1}{2} $ を満たさなければならない． 2. **中心**を表す区画 $ (x, y) $ を決める．ただし $ r+1 \leqq x \leqq N-r $ ， $ r+1 \leqq y \leqq N-r $ を満たさなければならない． 3. 色 $ c_0, c_1, c_2, \dots, c_r $ をそれぞれ赤・黄・青の中から選んで決める． 4. それぞれの区画 $ (x', y') $ について， $ d = |x'-x| + |y'-y| $ に応じて以下の規則で花を植える．ただし， $ |t| $ は $ t $ の絶対値を表す． - $ d \leqq r $ であるならば，区画 $ (x', y') $ には色 $ c_d $ の花を植える． - $ d > r $ であるならば，区画 $ (x', y') $ には花を植えない． 庭園の大きさ，各区画に植えることができる花の色の情報が与えられたとき，K 理事長が植えることができる花の数の最大値を求めるプログラムを作成せよ．

入力は以下の形式で与えられる． > $ N $ $ A_{1,1} $ $ A_{1,2} $ $ \cdots $ $ A_{1,N} $ $ A_{2,1} $ $ A_{2,2} $ $ \cdots $ $ A_{2,N} $ $ \vdots $ $ A_{N,1} $ $ A_{N,2} $ $ \cdots $ $ A_{N,N} $

K 理事長が植えることができる花の数の最大値を $ 1 $ 行で出力せよ．

### 小課題 1. ( $ 4 $ 点) $ N = 3 $ ． 2. ( $ 13 $ 点) $ N \leqq 50 $ ． 3. ( $ 17 $ 点) $ N \leqq 800 $ ． 4. ( $ 14 $ 点) $ A_{i, j} \neq $ `R` を満たす $ (i, j) $ ( $ 1 \leqq i \leqq N, 1 \leqq j \leqq N $ ) は $ 5 $ 個以下である． 5. ( $ 16 $ 点) どの $ (i, j) $ ( $ 1 \leqq i \leqq N-1, 1 \leqq j \leqq N-1 $ ) についても， $ A_{i, j} $ ， $ A_{i, j+1} $ ， $ A_{i+1, j} $ ， $ A_{i+1, j+1} $ の中に `R` が $ 3 $ 個以上存在する． 6. 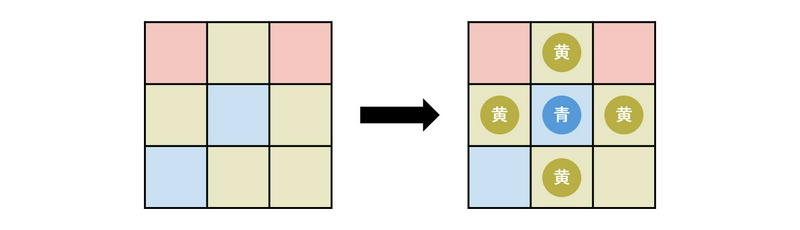( $ 36 $ 点) 追加の制約はない． ### Sample Explanation 1 $ r = 1 $ ， $ (x, y) = (2, 2) $ とし， $ c_0 $ として青， $ c_1 $ として黄を選ぶと，下図のように $ 5 $ 本の花を植えることができる．ただし，背景色は各区画に植えることができる花の色を示している．  $ 6 $ 本以上の花を植える方法は存在しないため， $ 5 $ を出力する． この入力例は小課題 $ 1, 2, 3, 6 $ の制約を満たす． ### Sample Explanation 2 $ r = 3 $ ， $ (x, y) = (5, 6) $ とし， $ c_0 $ として黄， $ c_1 $ として黄， $ c_2 $ として赤， $ c_3 $ として青を選ぶと，下図のように $ 25 $ 本の花を植えることができる．ただし，背景色は各区画に植えることができる花の色を示している．  $ 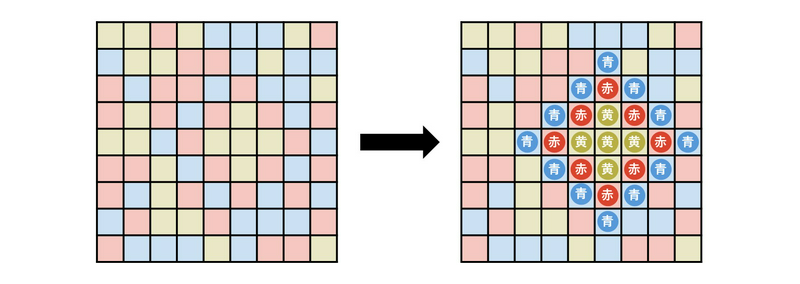26 $ 本以上の花を植える方法は存在しないため， $ 25 $ を出力する． この入力例は小課題 $ 2, 3, 6 $ の制約を満たす． ### Sample Explanation 3 この入力例は小課題 $ 2, 3, 6 $ の制約を満たす． ### Sample Explanation 4 この入力例は小課題 $ 2, 3, 4, 5, 6 $ の制約を満たす． ### Sample Explanation 5 この入力例は小課題 $ 2, 3, 5, 6 $ の制約を満たす． ### Constraints - $ 3 \leqq N \leqq 3\,500 $ ． - $ A_{i, j} $ は `R`，`Y`，`B` のいずれかである ( $ 1 \leqq i \leqq N, 1 \leqq j \leqq N $ )． - $ N $ は整数である．