AT_joi2024_yo2_e 高速道路の通行料金 (Highway Tolls)

JOI 王国は $ N $ 個の都市からなる王国であり，これらの都市には $ 1 $ から $ N $ までの番号が付けられている． JOI 王国には，これらの都市を結ぶ**一方通行**の高速道路が $ M $ 本あり， $ 1 $ から $ M $ までの番号が付けられている． 高速道路 $ i $ ( $ 1 \leqq i \leqq M $ ) を通ると都市 $ A_i $ から都市 $ B_i $ に移動することができ，通行にかかる時間は $ L_i $ である． それぞれの高速道路を通るたびに，通行料金が発生する． 高速道路 $ i $ の通行料金は最も安い時で $ C_i $ だが，JOI 王国の労働者は皆時間外労働を嫌うため，ある基準となる時刻 $ 0 $ から離れれば離れるほど通行料金が増えてしまう． 具体的には，都市 $ A_i $ を時刻 $ t $ に出発して高速道路 $ i $ を通行した場合，通行料金は定数 $ K $ を用いて $ C_i + K\times |t| $ と表される． ただし， $ |t| $ は $ t $ の絶対値を表す． 都市 $ 1 $ に住んでいるあなたは，友達の住む都市 $ N $ へ出かける計画を立てている． あなたは高速道路を通って都市 $ 1 $ から都市 $ N $ まで移動したいので，まずはそれが可能かどうか確かめ，可能ならば通行料金の総和が最小でいくらになるかも求めたい． ただし，移動経路や各都市を出発するタイミングは自由に決めることができる． 特に，都市 $ 1 $ を負の時刻に出発したり，高速道路を通行せずどこかの都市に留まっている時間があったりしてもよい． 高速道路の情報および定数 $ K $ が与えられたとき，高速道路を通って都市 $ 1 $ から都市 $ N $ まで移動することが可能かどうか判定し， 可能な場合は通行料金の総和の最小値を求めるプログラムを作成せよ． なお，この問題の制約の下では，高速道路を通って都市 $ 1 $ から都市 $ N $ まで移動することが可能な場合，通行料金の総和の最小値は必ず整数になることが証明できる．

入力は以下の形式で与えられる． > $ N $ $ M $ $ K $ $ A_1 $ $ B_1 $ $ L_1 $ $ C_1 $ $ A_2 $ $ B_2 $ $ L_2 $ $ C_2 $ $ \vdots $ $ A_M $ $ B_M $ $ L_M $ $ C_M $

高速道路を通って都市 $ 1 $ から都市 $ N $ まで移動することが不可能な場合は，`-1` を出力せよ． 可能な場合は，通行料金の総和の最小値を表す整数を $ 1 $ 行で出力せよ．

### 小課題 1. ( $ 9 $ 点) $ N \leqq 100 $ ， $ M \leqq 200 $ ， $ K = 0 $ ． 2. ( $ 21 $ 点) $ N \leqq 100 $ ， $ M \leqq 200 $ ， $ L_i \leqq 20 $ ( $ 1 \leqq i \leqq M $ )． 3. ( $ 13 $ 点) $ N \leqq 100 $ ， $ M = N - 1 $ ， $ A_i = i $ ， $ B_i = i+1 $ ( $ 1 \leqq i \leqq M $ )． 4. ( $ 23 $ 点) $ N \leqq 100 $ ， $ M \leqq 200 $ であり，以下の制約を満たす． - $ N $ は偶数， $ \lfloor \frac{B_i}{2} \rfloor - \lfloor \frac{A_i}{2} \rfloor = 1 $ ( $ 1 \leqq i \leqq M $ )． ここで， $ \lfloor x \rfloor $ は $ x $ 以下の最大の整数を表す． 5. ( $ 16 $ 点) $ N \leqq 100 $ ， $ M \leqq 200 $ ． 6. ( $ 11 $ 点) $ N \leqq 1\,500 $ ， $ M \leqq 3\,000 $ ． 7. 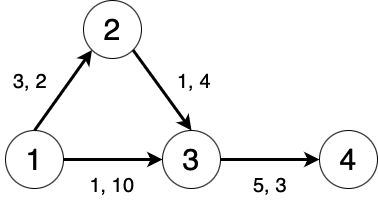( $ 7 $ 点) 追加の制約はない． ### Sample Explanation 1 JOI 王国の都市と道路の様子を図にすると以下のようになる． 丸は都市を，矢印は道路を表し，各道路の横にはその道路の $ L_i $ と $ C_i $ の値がこの順に書かれている． なお，丸の中に書かれた数字はその都市の番号を表す．  以下のように移動すると通行料金の総和が $ 15 $ になる． - 時刻 $ -1 $ : 都市 $ 1 $ を出発し，都市 $ 3 $ へ向かう．通行料金が $ 10+2\times \left|-1\right|=12 $ かかる． - 時刻 $ 0 $ : 都市 $ 3 $ に到着し，すぐに都市 $ 4 $ へ向かう．通行料金が $ 3+2\times |0|=3 $ かかる． - 時刻 $ 5 $ : 都市 $ 4 $ に到着する． 通行料金の総和が $ 15 $ より小さくなるような移動方法は存在しないため， $ 15 $ を出力する． この入力例は小課題 $ 2,5,6,7 $ の制約を満たす． ### Sample Explanation 2 入力例 $ 1 $ とは $ K $ の値だけが異なる． 以下のように移動すると通行料金の総和が $ 9 $ になる． - 時刻 $ -3 $ : 都市 $ 1 $ を出発し，都市 $ 2 $ へ向かう．通行料金が $ 2+0\times \left|-3\right|=2 $ かかる． - 時刻 $ 0 $ : 都市 $ 2 $ に到着し，すぐに都市 $ 3 $ へ向かう．通行料金が $ 4+0\times |0|=4 $ かかる． - 時刻 $ 1 $ : 都市 $ 3 $ に到着し，そのまま都市 $ 3 $ に留まる． - 時刻 $ 3 $ : 都市 $ 3 $ を出発し，都市 $ 4 $ へ向かう．通行料金が $ 3+0\times |3|=3 $ かかる． - 時刻 $ 8 $ : 都市 $ 4 $ に到着する． 通行料金の総和が $ 9 $ より小さくなるような移動方法は存在しないため， $ 9 $ を出力する． この入力例は小課題 $ 1,2,5,6,7 $ の制約を満たす． ### Sample Explanation 3 高速道路を通って都市 $ 1 $ から都市 $ 2 $ まで移動することは不可能なので，`-1` を出力する． この入力例は小課題 $ 2,5,6,7 $ の制約を満たす． ### Sample Explanation 4 この入力例は小課題 $ 2,3,5,6,7 $ の制約を満たす． ### Sample Explanation 5 同じ $ (A_i,B_i) $ のペアを持つ複数の道路が存在することもある． この入力例は小課題 $ 2,4,5,6,7 $ の制約を満たす． ### Sample Explanation 6 この入力例は小課題 $ 5,6,7 $ の制約を満たす． ### Constraints - $ 2 \leqq N \leqq 4\,000 $ ． - $ 1 \leqq M \leqq 8\,000 $ ． - $ 0 \leqq K \leqq 100\,000 $ ． - $ 1 \leqq A_i \leqq N $ ( $ 1 \leqq i \leqq M $ )． - $ 1 \leqq B_i \leqq N $ ( $ 1 \leqq i \leqq M $ )． - $ A_i \neq B_i $ ( $ 1 \leqq i \leqq M $ )． - $ 1 \leqq L_i \leqq 1\,000\,000 $ ( $ 1 \leqq i \leqq M $ )． - $ 0 \leqq C_i \leqq 10^9 $ ( $ 1 \leqq i \leqq M $ )． - 入力される値はすべて整数である．