AT_joi2024ho_e 道路網の整備 2 (Road Service 2)

JOI 市には，無限に長い $ H $ 本の東西方向の道路と $ W $ 本の南北方向の道路からなる格子状の道路網がある．北から $ i $ 本目 ( $ 1 \leqq i \leqq H $ ) の東西方向の道路と，西から $ j $ 本目 ( $ 1 \leqq j \leqq W $ ) の南北方向の道路が交わる交差点を交差点 $ (i, j) $ と呼ぶことにする． 現在，道路の一部は整備不良により通行止めになっている．具体的な通行止めの状況は以下の通りである． - 北から $ i $ 本目 ( $ 1 \leqq i \leqq H $ ) の東西方向の道路の，交差点 $ (i, j) $ と交差点 $ (i, j + 1) $ を繋ぐ部分 ( $ 1 \leqq j \leqq W - 1 $ ) は， $ A_{i, j} = 0 $ のとき通行止めで， $ A_{i, j} = 1 $ のとき通行可能である． - 西から $ j $ 本目 ( $ 1 \leqq j \leqq W $ ) の南北方向の道路の，交差点 $ (i, j) $ と交差点 $ (i + 1, j) $ を繋ぐ部分 ( $ 1 \leqq i \leqq H - 1 $ ) は， $ B_{i, j} = 0 $ のとき通行止めで， $ B_{i, j} = 1 $ のとき通行可能である． - 道路のその他の部分，すなわち $ H \times W $ 個の交差点の外側の部分はすべて通行止めである． JOI 市の市長である K 理事長は，この道路網の**整備計画**を作ることにした．整備計画は， $ 0 $ 回以上の**整備**からなる． $ 1 $ 回の整備では， $ 1 \leqq i \leqq H $ を満たす整数 $ i $ を $ 1 $ つ選び，以下のことを行う： $ 1 \leqq j \leqq W - 1 $ を満たす**すべての**整数 $ j $ について，北から $ i $ 本目の東西方向の道路の，交差点 $ (i, j) $ と交差点 $ (i, j + 1) $ を繋ぐ部分を（もし通行止めであれば）通行可能にする．これには全体で $ C_i $ 日間かかる．ただし， $ C_i $ は $ 1 $ または $ 2 $ である． 整備計画に含まれる複数の整備を同時に並行して行うことはできない．したがって，整備計画の実行に必要な日数は，整備計画に含まれるすべての整備にかかる日数の合計である． K 理事長は，まず市の重要施設の間を行き来できるようにするため，あなたに $ Q $ 個の質問をした． $ k $ 個目 ( $ 1 \leqq k \leqq Q $ ) の質問は以下のようなものである． $ T_k $ 個の交差点 $ (X_{k, 1}, Y_{k, 1}), (X_{k, 2}, Y_{k, 2}), \dots, (X_{k, T_k}, Y_{k, T_k}) $ の間を，道路の通行可能な部分のみを通って行き来できるようにするような整備計画は存在するか． 存在するならば，そのような整備計画の実行に必要な日数として考えられる最小値は何日間か． 道路網の通行止めの状況，東西方向の各道路の整備にかかる日数，K 理事長の質問の内容が与えられたとき，K 理事長の質問にすべて答えるプログラムを作成せよ． ---

入力は以下の形式で標準入力から与えられる． > $ H $ $ W $ $ Q $ $ A_{1,1}A_{1,2}\cdots A_{1,W - 1} $ $ A_{2,1}A_{2,2}\cdots A_{2,W - 1} $ $ \vdots $ $ A_{H,1}A_{H,2}\cdots A_{H,W - 1} $ $ B_{1,1}B_{1,2}\cdots B_{1,W} $ $ B_{2,1}B_{2,2}\cdots B_{2,W} $ $ \vdots $ $ B_{H - 1,1}B_{H - 1,2}\cdots B_{H - 1,W} $ $ C_1 $ $ C_2 $ $ \cdots $ $ C_H $ $ \mathrm{Query}_1 $ $ \mathrm{Query}_2 $ $ \vdots $ $ \mathrm{Query}_Q $ ただし，各 $ \mathrm{Query}_k $ ( $ 1 \leqq k \leqq Q $ ) は以下の形式である． > $ T_k $ $ X_{k,1} $ $ Y_{k,1} $ $ X_{k,2} $ $ Y_{k,2} $ $ \vdots $ $ X_{k,T_k} $ $ Y_{k,T_k} $

標準出力に $ Q $ 行で出力せよ． $ k $ 行目 ( $ 1 \leqq k \leqq Q $ ) には， $ T_k $ 個の交差点 $ (X_{k, 1}, Y_{k, 1}), (X_{k, 2}, Y_{k, 2}), \dots, (X_{k, T_k}, Y_{k, T_k}) $ の間を， 道路の通行可能な部分のみを通って行き来できるようにするような整備計画が存在するならば，そのような整備計画の実行に必要な日数の最小値を出力し，そうでないならば `-1` を出力せよ． ---

### 小課題 1. ( $ 10 $ 点) $ C_i = 1 $ ( $ 1 \leqq i \leqq H $ )， $ Q \leqq 5 $ ， $ T_k = 2 $ ( $ 1 \leqq k \leqq Q $ )， $ A_{i, j} = 0 $ ( $ 1 \leqq i \leqq H, 1 \leqq j \leqq W - 1 $ )． 2. ( $ 6 $ 点) $ C_i = 1 $ ( $ 1 \leqq i \leqq H $ )， $ Q \leqq 5 $ ， $ T_k = 2 $ ( $ 1 \leqq k \leqq Q $ )． 3. ( $ 15 $ 点) $ C_i = 1 $ ( $ 1 \leqq i \leqq H $ )， $ Q \leqq 5 $ ． 4. ( $ 11 $ 点) $ C_i = 1 $ ( $ 1 \leqq i \leqq H $ )， $ T_k = 2 $ ( $ 1 \leqq k \leqq Q $ )． 5. ( $ 6 $ 点) $ C_i = 1 $ ( $ 1 \leqq i \leqq H $ )． 6. ( $ 12 $ 点) $ Q \leqq 5 $ ． 7. ( $ 26 $ 点) $ T_k = 2 $ ( $ 1 \leqq k \leqq Q $ )． 8. 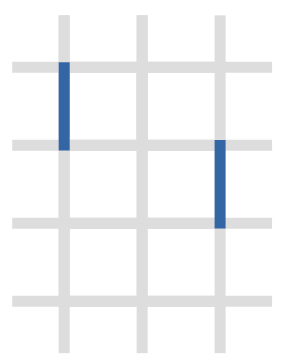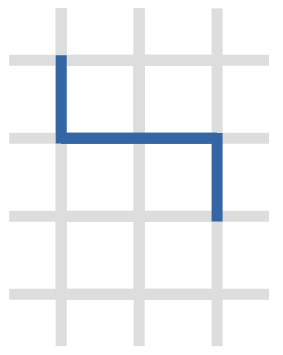( $ 14 $ 点) 追加の制約はない． --- ### Sample Explanation 1 以下の図は，現在の通行止めの状況である．灰色は通行止めを表し，青色は通行可能を表している．  - $ 1 $ 個目の質問では，整数 $ i $ として $ 2 $ を選ぶような整備を行うと通行止めの状況は下図のようになり，交差点 $ (1, 1), (3, 3) $ の間を互いに行き来できるようになる．  この $ 1 $ 回の整備のみからなる整備計画の実行に必要な日数は $ 1 $ であり，これより少ない日数で交差点 $ (1, 1), (3, 3) $ の間を互いに行き来できるようにするような整備計画は存在しないため， $ 1 $ を出力する． - $ 2 $ 個目の質問では，整数 $ i $ としてそれぞれ $ 1, 2, 3 $ を選ぶような $ 3 $ 回の整備を行うと，交差点 $ (3, 1), (1, 2) $ の間を互いに行き来できるようになる． この $ 3 $ 回の整備からなる整備計画の実行に必要な日数は $ 3 $ であり，これより少ない日数で交差点 $ (3, 1), (1, 2) $ の間を互いに行き来できるようにするような整備計画は存在しないため， $ 3 $ を出力する． - $ 3 $ 個目の質問では，整備を $ 1 $ 回も行わなくても交差点 $ (2, 3), (3, 3) $ の間を互いに行き来できるので， $ 0 $ を出力する． - $ 4 $ 個目の質問では，交差点 $ (4, 2), (3, 2) $ の間を互いに行き来できるようにするような整備計画は存在しないため， $ -1 $ を出力する． この入力例は小課題 $ 1, 2, 3, 4, 5, 6, 7, 8 $ の制約を満たす． --- ### Sample Explanation 2 この入力例は小課題 $ 2, 3, 4, 5, 6, 7, 8 $ の制約を満たす． --- ### Sample Explanation 3 この入力例は小課題 $ 3, 5, 6, 8 $ の制約を満たす． --- ### Sample Explanation 4 この入力例は小課題 $ 6, 7, 8 $ の制約を満たす． --- ### Sample Explanation 5 この入力例は小課題 $ 6, 8 $ の制約を満たす． ### Constraints - $ 2 \leqq H $ ． - $ 2 \leqq W $ ． - $ H \times W \leqq 1\,000\,000 $ ． - $ 1 \leqq Q \leqq 100\,000 $ ． - $ A_{i, j} $ は $ 0 $ または $ 1 $ ( $ 1 \leqq i \leqq H, 1 \leqq j \leqq W - 1 $ )． - $ B_{i, j} $ は $ 0 $ または $ 1 $ ( $ 1 \leqq i \leqq H - 1, 1 \leqq j \leqq W $ )． - $ C_i $ は $ 1 $ または $ 2 $ ( $ 1 \leqq i \leqq H $ )． - $ 2 \leqq T_k $ ( $ 1 \leqq k \leqq Q $ )． - $ T_1 + T_2 + \cdots + T_Q \leqq 200\,000 $ ． - $ 1 \leqq X_{k, l} \leqq H $ ( $ 1 \leqq k \leqq Q, 1 \leqq l \leqq T_k $ )． - $ 1 \leqq Y_{k, l} \leqq W $ ( $ 1 \leqq k \leqq Q, 1 \leqq l \leqq T_k $ )． - $ (X_{k, 1}, Y_{k, 1}), (X_{k, 2}, Y_{k, 2}), \dots, (X_{k, T_k}, Y_{k, T_k}) $ は相異なる ( $ 1 \leqq k \leqq Q $ )． - 入力される値はすべて整数である．