AT_joi2024ho_e 道路網の整備 2 (Road Service 2)

JOI 市有一个由无限延伸的 $H$ 条东西向道路和 $W$ 条南北向道路组成的网格状道路系统。北侧第 $i$ 条（$1 \leqslant i \leqslant H$）东西向道路和西侧第 $j$ 条（$1 \leqslant j \leqslant W$）南北向道路的交点称为交叉点 $(i, j)$。 当前，部分道路由于维护不善而封闭，具体的封闭情况如下： - 北侧第 $i$ 条（$1 \leqslant i \leqslant H$）东西向道路上，连接交叉点 $(i, j)$ 和 $(i, j+1)$ 的路段（$1 \leqslant j \leqslant W-1$），在 $A_{i, j} = 0$ 时封闭，$A_{i, j} = 1$ 时可通行。 - 西侧第 $j$ 条（$1 \leqslant j \leqslant W$）南北向道路上，连接交叉点 $(i, j)$ 和 $(i+1, j)$ 的路段（$1 \leqslant i \leqslant H - 1$），在 $B_{i, j} = 0$ 时封闭，$B_{i, j} = 1$ 时可通行。 - 其他部分，即 $H \times W$ 个交叉点以外的部分全部封闭。 JOI 市的市长 K 理事长打算拟定这个道路网的**整修计划**。一次整修计划包含 $0$ 次或多次**整修**。每进行一次整修，选择一个整数 $i$ （$1 \leqslant i \leqslant H$），对于所有 $1 \leqslant j \leqslant W-1$，会将北侧第 $i$ 条东西向道路上，连接交叉点 $(i, j)$ 和 $(i, j+1)$ 的所有路段（如果封闭，则开放），该操作总共需要 $C_{i}$ 天。这里 $C_i$ 为 $1$ 或 $2$。 同一整修计划中的多个整修不能同时进行。因此，执行整修计划所需的天数为所有包含的整修的天数之和。 为了先保证城市重要机构之间的流通，K 理事长向你提出了 $Q$ 个问题。第 $k$ 个（$1 \leqslant k \leqslant Q$）问题如下： 是否存在一个整修计划，使得 $T_k$ 个交叉点 $(X_{k, 1}, Y_{k, 1}), (X_{k, 2}, Y_{k, 2}), \dots, (X_{k, T_k}, Y_{k, T_k})$ 之间能够通过通畅的道路互相到达？如果存在，执行这样整修计划所需的最短天数是多少？ 给定道路网的封闭状况、东西向每条道路的整修所需天数，以及所有 K 理事长的问题，请你编写程序输出所有问题的答案。 ---

输入通过标准输入按如下格式给出： > $H$ $W$ $Q$ $A_{1,1}A_{1,2}\cdots A_{1,W - 1}$ $A_{2,1}A_{2,2}\cdots A_{2,W - 1}$ $\vdots$ $A_{H,1}A_{H,2}\cdots A_{H,W - 1}$ $B_{1,1}B_{1,2}\cdots B_{1,W}$ $B_{2,1}B_{2,2}\cdots B_{2,W}$ $\vdots$ $B_{H - 1,1}B_{H - 1,2}\cdots B_{H - 1,W}$ $C_1$ $C_2$ $\cdots$ $C_H$ $\mathrm{Query}_1$ $\mathrm{Query}_2$ $\vdots$ $\mathrm{Query}_Q$ 每个 $\mathrm{Query}_k$（$1 \leqslant k \leqslant Q$）的格式如下： > $T_k$ $X_{k,1}$ $Y_{k,1}$ $X_{k,2}$ $Y_{k,2}$ $\vdots$ $X_{k,T_k}$ $Y_{k,T_k}$

请按顺序输出 $Q$ 行。第 $k$ 行（$1 \leqslant k \leqslant Q$）输出：如果存在能够使 $T_k$ 个交叉点 $(X_{k, 1}, Y_{k, 1}), (X_{k, 2}, Y_{k, 2}), \dots, (X_{k, T_k}, Y_{k, T_k})$ 互相连通的整修计划，则输出所需天数的最小值；否则输出 `-1`。 ---

### 子任务 1. ($10$ 分) $C_i = 1$（$1 \leqslant i \leqslant H$），$Q \leqslant 5$，$T_k = 2$（$1 \leqslant k \leqslant Q$），$A_{i, j} = 0$（$1 \leqslant i \leqslant H, 1 \leqslant j \leqslant W - 1$）。 2. ($6$ 分) $C_i = 1$（$1 \leqslant i \leqslant H$），$Q \leqslant 5$，$T_k = 2$（$1 \leqslant k \leqslant Q$）。 3. ($15$ 分) $C_i = 1$（$1 \leqslant i \leqslant H$），$Q \leqslant 5$。 4. ($11$ 分) $C_i = 1$（$1 \leqslant i \leqslant H$），$T_k = 2$（$1 \leqslant k \leqslant Q$）。 5. ($6$ 分) $C_i = 1$（$1 \leqslant i \leqslant H$）。 6. ($12$ 分) $Q \leqslant 5$。 7. ($26$ 分) $T_k = 2$（$1 \leqslant k \leqslant Q$）。 8. ($14$ 分) 无额外限制。 --- ### 样例解释 1 以下是当前的道路封闭状况。灰色表示封闭，蓝色表示可通行。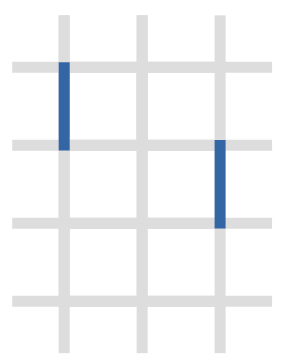  - 第 $1$ 个询问中，若选择 $i=2$ 进行整修，则整修后的道路状况如下图所示，交叉点 $(1, 1)$、$(3, 3)$ 可以互相连通。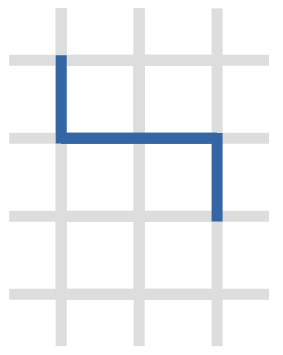  这个仅包含一次整修的整修计划需要 $1$ 天，且不存在更短时间能让这两点连通的方案，因此输出 $1$。 - 第 $2$ 个询问，若对 $i=1,2,3$ 依次进行三次整修，可以让 $(3,1)$、$(1,2)$ 互通。此时所需天数为 $3$，不存在更优答案，因此输出 $3$。 - 第 $3$ 个询问，两点 $(2,3),(3,3)$ 已经连通，无需整修，输出 $0$。 - 第 $4$ 个询问，无法让 $(4,2),(3,2)$ 连通，因此输出 $-1$。 本例输入满足子任务 $1,2,3,4,5,6,7,8$ 的限制。 --- ### 样例解释 2 本例输入满足子任务 $2,3,4,5,6,7,8$ 的限制。 --- ### 样例解释 3 本例输入满足子任务 $3,5,6,8$ 的限制。 --- ### 样例解释 4 本例输入满足子任务 $6,7,8$ 的限制。 --- ### 样例解释 5 本例输入满足子任务 $6,8$ 的限制。 ### 数据范围 - $2 \leqslant H$。 - $2 \leqslant W$。 - $H \times W \leqslant 1\,000\,000$。 - $1 \leqslant Q \leqslant 100\,000$。 - $A_{i, j}$ 为 $0$ 或 $1$，$1 \leqslant i \leqslant H, 1 \leqslant j \leqslant W-1$。 - $B_{i, j}$ 为 $0$ 或 $1$，$1 \leqslant i \leqslant H-1, 1 \leqslant j \leqslant W$。 - $C_i$ 为 $1$ 或 $2$，$1 \leqslant i \leqslant H$。 - $2 \leqslant T_k$，$1 \leqslant k \leqslant Q$。 - $T_1+T_2+\cdots+T_Q \leqslant 200\,000$。 - $1 \leqslant X_{k, l} \leqslant H$，$1 \leqslant k \leqslant Q, 1 \leqslant l \leqslant T_k$。 - $1 \leqslant Y_{k, l} \leqslant W$，$1 \leqslant k \leqslant Q, 1 \leqslant l \leqslant T_k$。 - $(X_{k, 1}, Y_{k, 1}),\dots,(X_{k, T_k}, Y_{k, T_k})$ 互不相同（$1 \leqslant k \leqslant Q$）。 - 所有输入均为整数。 由 ChatGPT 5 翻译