AT_joig2023_d コイン集め 2 (Coin Collecting 2)
Description
机の上に,縦 $ H $ 行,横 $ W $ 列の長方形状にコインが並べられている. 最初,上から $ i $ 行目 ( $ 1 \leqq i \leqq H $ ),左から $ j $ 列目 ( $ 1 \leqq j \leqq W $ ) のコインは, $ S_{i,j}= $ `#` のとき表面, $ S_{i,j}= $ `.` のとき裏面が見えている状態である.
葵と凛は,これらのコインを用いてゲームを行うことにした.ゲームは以下のような流れで行われる.
1. 葵がどれか $ 1 $ つの行を選び,その行のコインをすべてひっくり返す.
2. 凛がどれか $ 1 $ つの列を選び,その列のコインをすべてひっくり返す.
3. 葵が,表面が見えるコインをすべて獲得する.また凛が,裏面が見えるコインをすべて獲得する.
葵と凛はそれぞれ,できるだけ多くのコインを獲得したい.
ゲーム開始時のコインの状態が与えられたとき, 両者が最善を尽くした場合にそれぞれが獲得できるコインの枚数を求めるプログラムを作成せよ.
Input Format
入力は以下の形式で与えられる.
> $ H $ $ W $ $ S_{1,1} $ $ S_{1,2} $ $ \cdots $ $ S_{1,W} $ $ S_{2,1} $ $ S_{2,2} $ $ \cdots $ $ S_{2,W} $ $ \vdots $ $ S_{H,1} $ $ S_{H,2} $ $ \cdots $ $ S_{H,W} $
Output Format
葵と凛の得点をこの順に空白区切りで出力せよ.
Explanation/Hint
### 小課題
1. ( $ 2 $ 点) $ H = 1 $ , $ W = 1 $ .
2. ( $ 8 $ 点) $ H = 1 $ , $ W \leqq 40 $ .
3. ( $ 9 $ 点) $ H \leqq 40 $ , $ W = 1 $ .
4. ( $ 14 $ 点) $ H = 2 $ , $ W = 2 $ .
5. ( $ 23 $ 点) $ H \leqq 40 $ , $ W \leqq 40 $ .
6. ( $ 18 $ 点) $ H \leqq 250 $ , $ W \leqq 250 $ .
7. ( $ 26 $ 点) 追加の制約はない.
### Sample Explanation 1
この入力例では,必ず以下のようにゲームが進行する.
1. まず,葵が $ 1 $ 行目のすべてのコインをひっくり返す.
2. 次に,凛が $ 1 $ 列目のすべてのコインをひっくり返す.
このとき,唯一のコインの見える面は「表→裏→表」と変化するため,葵が $ 1 $ 枚のコインを獲得できるが,凛はコインを獲得できない.したがって, $ 1 $ , $ 0 $ をこの順に空白区切りで出力する.
なお,この入力例は小課題 $ 1, 2, 3, 5, 6, 7 $ の制約を満たす.
### Sample Explanation 2
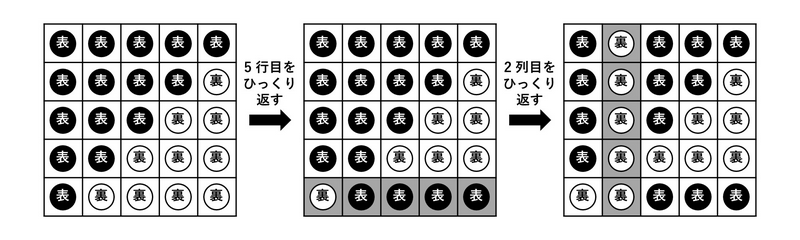
両者が最善を尽くした場合の,ゲームの進行の一例を下図に示す.
この入力例は小課題 $ 5, 6, 7 $ の制約を満たす.
### Sample Explanation 3
この入力例は小課題 $ 2, 5, 6, 7 $ の制約を満たす.
### Sample Explanation 4
この入力例は小課題 $ 3, 5, 6, 7 $ の制約を満たす.
### Sample Explanation 5
この入力例は小課題 $ 5, 6, 7 $ の制約を満たす.
### Sample Explanation 6
この入力例は小課題 $ 5, 6, 7 $ の制約を満たす.
### Constraints
- $ H \geqq 1 $ .
- $ W \geqq 1 $ .
- $ H \times W \leqq 500\,000 $ .
- $ S_{i, j} $ は `#`,`.` のいずれかである ( $ 1 \leqq i \leqq H $ , $ 1 \leqq j \leqq W $ ).
- $ H, W $ は整数である.