AT_joig2024_d たくさんの数字 (Many Digits)

JOI 高校の葵さんは， $ N $ 行 $ N $ 列のマス目の各マスに整数を十進数表記で書くことにした．具体的には上から $ i $ 行目 ( $ 1 \leqq i \leqq N $ )，左から $ j $ 列目 ( $ 1 \leqq j \leqq N $ ) のマスには $ A_i + B_j $ を十進数表記で書く． 葵さんは数字を何文字書くことになるかを知りたい．つまり，葵さんが書く $ N^2 $ 個の整数の桁数の合計を求めたい． $ A_i $ ( $ 1 \leqq i \leqq N $ ) と $ B_j $ ( $ 1 \leqq j \leqq N $ ) が与えられたとき，葵さんが書く $ N^2 $ 個の整数の桁数の合計を求めるプログラムを作成せよ．

入力は以下の形式で与えられる． > $ N $ $ A_1 $ $ A_2 $ $ \cdots $ $ A_N $ $ B_1 $ $ B_2 $ $ \cdots $ $ B_N $

葵さんが書く $ N^2 $ 個の整数の桁数の合計を $ 1 $ 行で出力せよ．

### 小課題 1. ( $ 5 $ 点) $ N = 1 $ ． 2. ( $ 11 $ 点) $ N \leqq 2\,000 $ ． 3. ( $ 15 $ 点) $ A_i \leqq 2\,000 $ ( $ 1 \leqq i \leqq N $ )， $ B_j \leqq 2\,000 $ ( $ 1 \leqq j \leqq N $ )． 4. ( $ 8 $ 点) $ 100\,000\,000 \leqq A_i \leqq 500\,000\,000 $ ( $ 1 \leqq i \leqq N $ )， $ 100\,000\,000 \leqq B_j \leqq 500\,000\,000 $ ( $ 1 \leqq j \leqq N $ )． 5. ( $ 22 $ 点) $ 100\,000\,000 \leqq A_i $ ( $ 1 \leqq i \leqq N $ )， $ 100\,000\,000 \leqq B_j $ ( $ 1 \leqq j \leqq N $ )． 6. ( $ 12 $ 点) $ A_i \leqq 150\,000 $ ( $ 1 \leqq i \leqq N $ )， $ B_j = j $ ( $ 1 \leqq j \leqq N $ )． 7. ( $ 13 $ 点) $ B_j = j $ ( $ 1 \leqq j \leqq N $ )． 8. 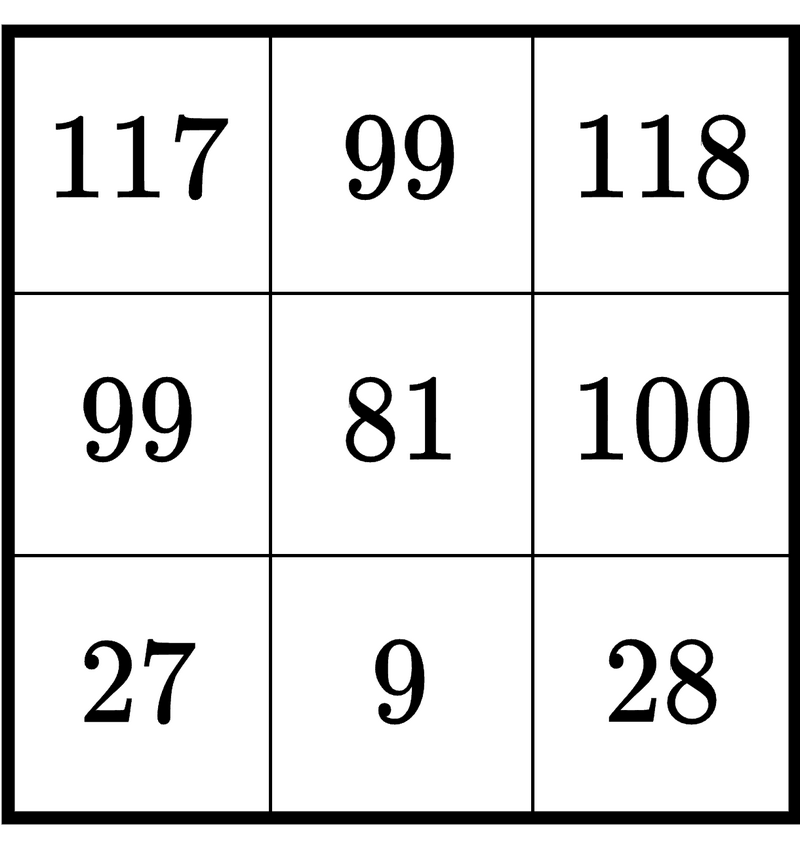( $ 14 $ 点) 追加の制約はない． ### Sample Explanation 1 葵さんが各マスに書く整数は以下の図のようになる．  例えば，葵さんは上から $ 1 $ 行目，左から $ 1 $ 列目のマスには $ A_1 + B_1 = 97 + 20 = 117 $ を書く．また，上から $ 3 $ 行目，左から $ 2 $ 列目のマスには $ A_3 + B_2 = 7 + 2 = 9 $ を書く． 葵さんが書く $ 9 $ 個の整数は $ 117, 99, 118, 99, 81, 100, 27, 9, 28 $ であり，それぞれの桁数は $ 3, 2, 3, 2, 2, 3, 2, 1, 2 $ である． よって，葵さんが書く $ 9 $ 個の整数の桁数の合計は $ 3 + 2 + 3 + 2 + 2 + 3 + 2 + 1 + 2 = 20 $ となるため， $ 20 $ を出力する． この入力例は小課題 $ 2, 3, 8 $ の制約を満たす． ### Sample Explanation 2 葵さんが各マスに書く数字は以下の図のようになる．  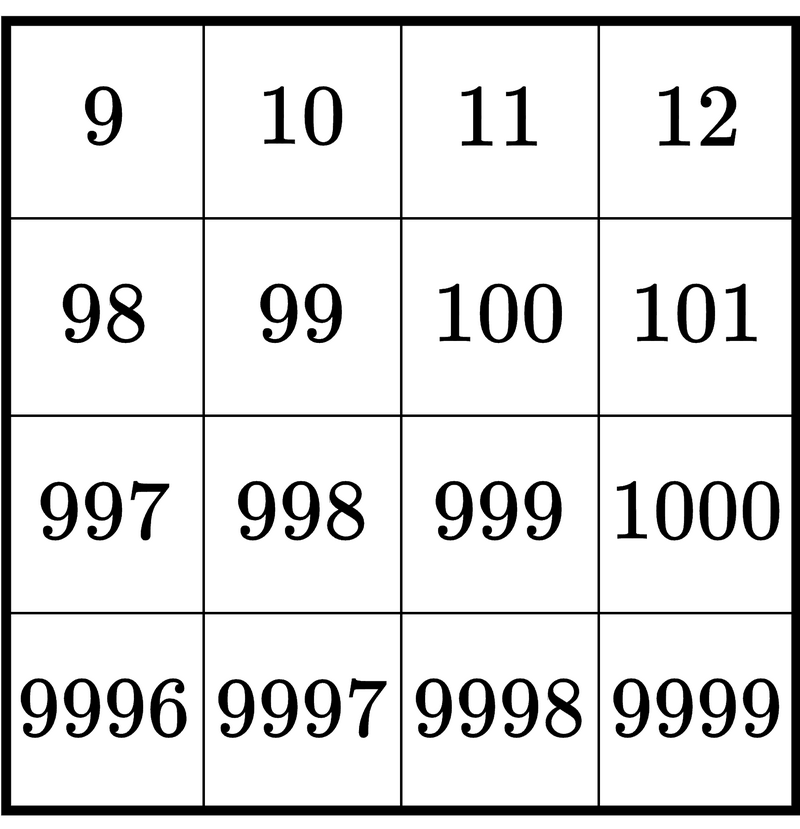例えば，葵さんは上から $ 2 $ 行目，左から $ 3 $ 列目のマスには $ A_2 + B_3 = 97 + 3 = 100 $ を書く．この整数の桁数は $ 3 $ である．また，上から $ 4 $ 行目，左から $ 2 $ 列目のマスには $ A_4 + B_2 = 9\,995 + 2 = 9\,997 $ を書く．この整数の桁数は $ 4 $ である． 葵さんが書く $ 16 $ 個の整数の桁数の合計は $ 46 $ となるため， $ 46 $ を出力する． この入力例は小課題 $ 2, 6, 7, 8 $ の制約を満たす． ### Sample Explanation 3 葵さんが書く整数は $ 1 $ 個で，その値は $ 500\,000\,000 + 500\,000\,000 = 1\,000\,000\,000 $ である．この整数の桁数は $ 10 $ である． よって，葵さんが書く $ 1 $ 個の整数の桁数の合計は $ 10 $ となるため， $ 10 $ を出力する． この入力例は小課題 $ 1, 2, 4, 5, 8 $ の制約を満たす． ### Sample Explanation 4 この入力例は小課題 $ 2, 5, 8 $ の制約を満たす． ### Constraints - $ 1 \leqq N \leqq 150\,000 $ ． - $ 1 \leqq A_i \leqq 999\,999\,999 $ ( $ 1 \leqq i \leqq N $ )． - $ 1 \leqq B_j \leqq 999\,999\,999 $ ( $ 1 \leqq j \leqq N $ )． - 入力される値はすべて整数である．