AT_joig2025_b ポスター 2 (Poster 2)

JOI 学園の理恵さんは，今年 $ 3 $ 月に実施される文化祭のポスターを作った． このポスターは $ N $ 行 $ N $ 列のマス目の形をしており，各マスは $ 1 $ から $ K $ までの番号が付けられた $ K $ 種類の色のいずれかで塗られている． 具体的には，ポスターの上から $ i $ 行目，左から $ j $ 列目 ( $ 1 \leqq i \leqq N $ ， $ 1 \leqq j \leqq N $ ) は色 $ A_{i,j} $ で塗られている． しかし，このポスターについて生徒間で話し合いを行ったところ，もう少しカラフルにした方が良いのではないかという意見が出た． 具体的には，以下で定義される**カラフル度**を上げた方が良いのではないかという意見が出た． - 連続する $ 2 $ 行 $ 2 $ 列の正方形領域のうち， $ 3 $ 種類以上の色を含むものの個数． たとえば，下図左のようなポスターを作った場合，下図右に示す $ 2 $ つの長方形領域について $ 3 $ 種類以上の色を含むため，カラフル度は $ 2 $ である．  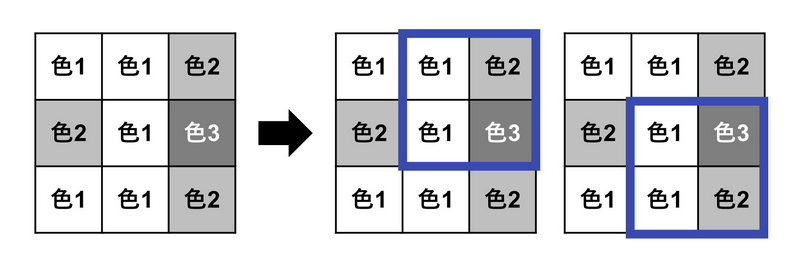ポスターの提出期限まであと数分しかないので，以下の操作を $ 0 $ 回または $ 1 $ 回行うことで，カラフル度を最大化したい． - 好きなマスを $ 1 $ つ選び，そのマスの色を $ K $ 種類の色のいずれかで塗り替える． 理恵さんが最初に作ったポスターの情報が与えられるので，達成できるカラフル度の最大値を求めるプログラムを作成せよ．

入力は以下の形式で与えられる． > $ N $ $ K $ $ A_{1,1} $ $ A_{1,2} $ $ \cdots $ $ A_{1,N} $ $ A_{2,1} $ $ A_{2,2} $ $ \cdots $ $ A_{2,N} $ $ \vdots $ $ A_{N,1} $ $ A_{N,2} $ $ \cdots $ $ A_{N,N} $

達成できるカラフル度の最大値を $ 1 $ 行で出力せよ．

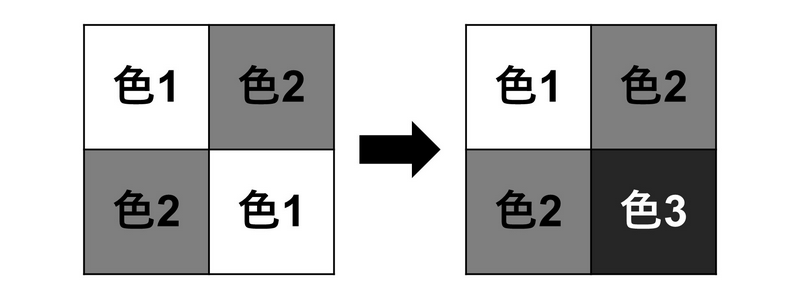
### 小課題 1. ( $ 9 $ 点) $ N = 2 $ ， $ K = 3 $ ． 2. ( $ 6 $ 点) $ A_{i,j} $ ( $ 1 \leqq i \leqq N $ ， $ 1 \leqq j \leqq N $ ) はすべて異なる． 3. ( $ 27 $ 点) $ N \leqq 10 $ ， $ K \leqq 10 $ ． 4. ( $ 26 $ 点) $ N \leqq 10 $ ． 5. 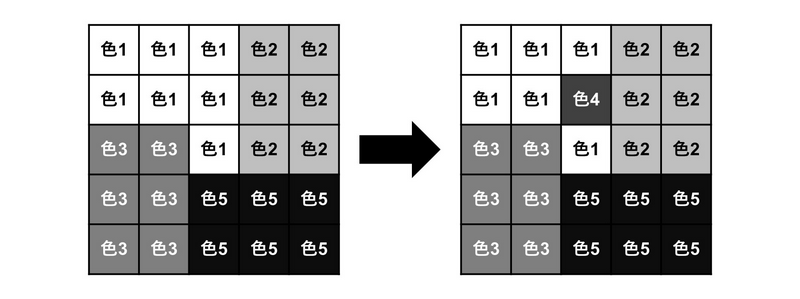( $ 32 $ 点) 追加の制約はない． ### Sample Explanation 1 以下のように，上から $ 2 $ 行目，左から $ 2 $ 列目のマスを色 $ 3 $ で塗り替えることで，カラフル度 $ 1 $ を達成することができる．  カラフル度 $ 2 $ 以上を達成する方法はないため， $ 1 $ を出力する． この入力例は小課題 $ 1, 3, 4, 5 $ の制約を満たす． ### Sample Explanation 2 以下のように，上から $ 2 $ 行目，左から $ 3 $ 列目のマスを色 $ 4 $ で塗り替えることで，カラフル度 $ 5 $ を達成することができる．  カラフル度 $ 6 $ 以上を達成する方法はないため， $ 5 $ を出力する． この入力例は小課題 $ 3, 4, 5 $ の制約を満たす． ### Sample Explanation 3 この入力例は小課題 $ 2, 4, 5 $ の制約を満たす． ### Sample Explanation 4 この入力例は小課題 $ 3, 4, 5 $ の制約を満たす． ### Sample Explanation 5 この入力例は小課題 $ 4, 5 $ の制約を満たす． ### Constraints - $ 2 \leqq N \leqq 270 $ ． - $ 3 \leqq K \leqq 10^9 $ ． - $ 1 \leqq A_{i,j} \leqq K $ ( $ 1 \leqq i \leqq N $ ， $ 1 \leqq j \leqq N $ )． - 入力される値はすべて整数である．