AT_joigsp2025_f 日本浮上 (Japan Emerges)

日本列島は地殻変動の盛んな列島である． 日本列島のある海域は南北 $ H $ 行，東西 $ W $ 列のマス目で表される． 北から $ r $ 行目，西から $ c $ 列目 ( $ 1 \leqq r \leqq H $ ， $ 1 \leqq c \leqq W $ ) のマスをマス $ (r,c) $ と書く． 各マスは **陸** または **海** のいずれかである． 最初に海域に存在する陸はちょうど $ N $ マスであり，それ以外のマスは海である． 最初の時点でそれらの陸の位置はマス $ (R_1, C_1), (R_2, C_2), \dots, (R_N, C_N) $ である． 日本列島では毎日正午に地殻変動が起こる． $ t $ 日目 $ (t \geqq 1) $ の正午に起こる地殻変動は以下のように表される． - $ 1 \leqq r \leqq H-1 $ ， $ 1 \leqq c \leqq W $ のうち $ t $ 日目の朝にマス $ (r, c) $ が陸でマス $ (r+1, c) $ が海であるようなすべての $ (r, c) $ について，マス $ (r+1, c) $ が新たに陸となる． どの陸からどの陸へも東西南北に隣り合っている陸のみを辿って到達できる場合，日本列島は連結であると定める． 地殻変動が進むにつれ日本列島が連結になることがある． 最初の時点での海域の情報が与えられたとき，地殻変動が繰り返されることで日本列島が連結になることがあるか判定し，連結になる場合には何回の地殻変動後に初めて連結になるかを求めるプログラムを作成せよ． ---

入力は以下の形式で標準入力から与えられる． > $ H $ $ W $ $ N $ $ R_1 $ $ C_1 $ $ R_2 $ $ C_2 $ $ \vdots $ $ R_N $ $ C_N $

標準出力に，日本列島が連結になる場合には何回の地殻変動後に初めて連結になるかを $ 1 $ 行で出力せよ． ただし，最初の時点で連結である場合は `0` を出力せよ． また，この先日本列島が連結になることがない場合は `-1` を出力せよ．

### 小課題 1. ( $ 5 $ 点) $ W = 1 $ ． 2. ( $ 9 $ 点) $ N = 2 $ ． 3. ( $ 8 $ 点) $ H \leqq 500 $ ， $ W \leqq 500 $ ， $ N \leqq 500 $ ． 4. ( $ 28 $ 点) $ N \leqq 2\,000 $ ． 5. ( $ 13 $ 点) $ H \times W \leqq 200\,000 $ ． 6. ( $ 13 $ 点) $ H \times N \leqq 200\,000 $ ． 7. 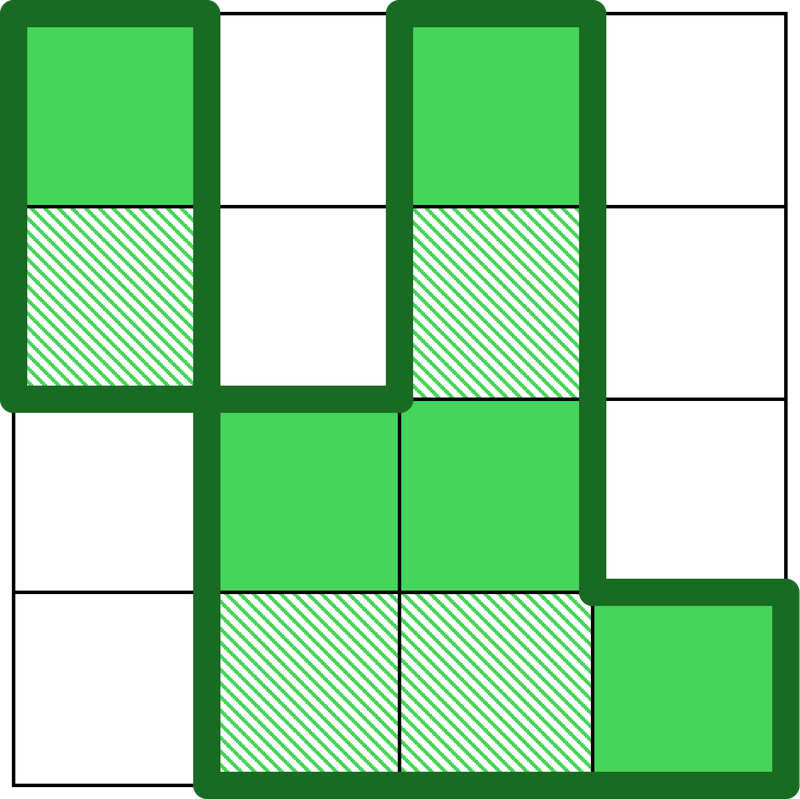( $ 24 $ 点) 追加の制約はない． --- ### Sample Explanation 1 以下の図は最初の時点での海域の状況である．塗りつぶされたマスが陸を表し，空白のマスが海を表す．  $ 1 $ 回目の地殻変動で新たに陸となるのはマス $ (2, 1), (2, 3), (4, 2), (4, 3) $ の $ 4 $ 個である． $ 1 $ 回目の地殻変動の直後ではマス $ (1, 1) $ からマス $ (4, 4) $ などに東西南北に隣り合っている陸のみを辿って到達できないため，日本列島は連結ではない． 以下の図は $ 1 $ 回目の地殻変動の直後の海域の状況である．新たに斜線部のマスが陸となり，それ以外のマスは変化しない．  $ 2 $ 回目の地殻変動で新たに陸となるのはマス $ (3, 1) $ の $ 1 $ 個である． $ 2 $ 回目の直後の海域の状況は以下の図のようになる．  $ 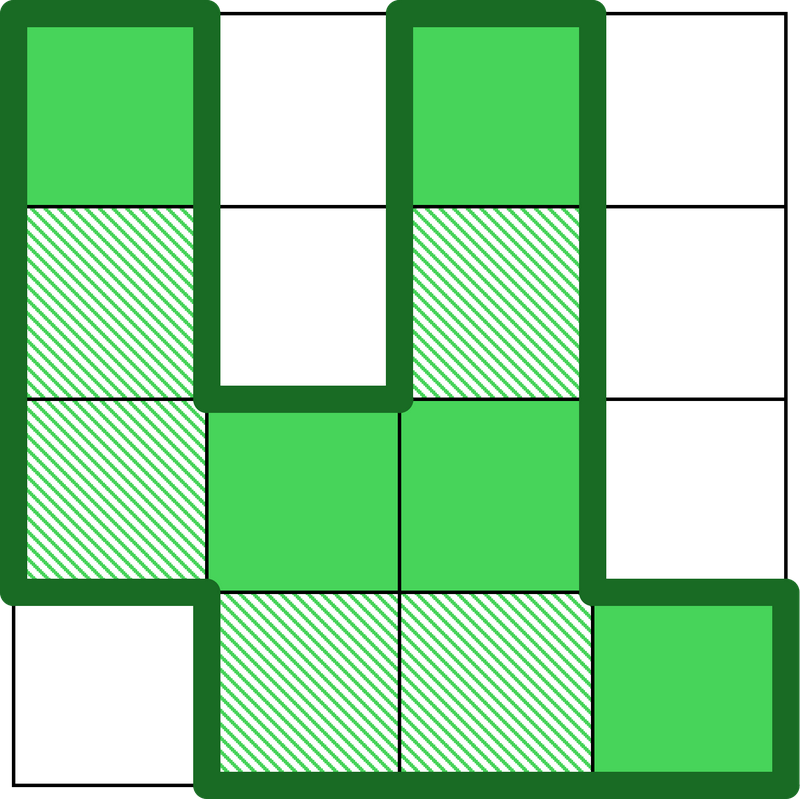2 $ 回目の地殻変動で初めて日本列島が連結になるため， $ 2 $ を出力する． この入力例は小課題 $ 3, 4, 5, 6, 7 $ の制約を満たす． --- ### Sample Explanation 2 日本列島が連結になることはないため，`-1` を出力する． この入力例は小課題 $ 2, 3, 4, 5, 6, 7 $ の制約を満たす． --- ### Sample Explanation 3 地殻変動が起こる前から日本列島は連結であるため，`0` を出力する． この入力例は小課題 $ 2, 3, 4, 5, 6, 7 $ の制約を満たす． ### Constraints - $ 1 \leqq H \leqq 200\,000 $ ． - $ 1 \leqq W \leqq 200\,000 $ ． - $ 2 \leqq N \leqq \min(H \times W,\ 200\,000) $ ． - $ 1 \leqq R_i \leqq H $ ( $ 1 \leqq i \leqq N $ )． - $ 1 \leqq C_i \leqq W $ ( $ 1 \leqq i \leqq N $ )． - $ (R_i, C_i) \neq (R_j, C_j) $ ( $ 1 \leqq i < j \leqq N $ )． - 入力される値はすべて整数である．