AT_joigsp2025_f 日本浮上 (Japan Emerges)

日本列岛是地壳运动频繁的列岛。日本列岛位于某片海域，这片海域可以用南北 $H$ 行、东西 $W$ 列的格子表示。从北起第 $r$ 行、西起第 $c$ 列（$1 \leq r \leq H$，$1 \leq c \leq W$）的格子记作格子 $(r,c)$。每个格子要么是**陆地**，要么是**海洋**。初始时，这片海域中恰好有 $N$ 个格子是陆地，其余的格子都是海洋。初始时这些陆地的位置分别是格子 $(R_1, C_1), (R_2, C_2), \dots, (R_N, C_N)$。 在日本列岛，每天中午都会发生一次地壳变动。第 $t$ 天（$t \geq 1$）中午发生的地壳变动如下所述： - 对于 $1 \leq r \leq H-1$，$1 \leq c \leq W$，若第 $t$ 天早晨格子 $(r, c)$ 是陆地且格子 $(r+1, c)$ 是海洋，则把所有这样的 $(r, c)$ 的 $(r+1, c)$ 变为新的陆地。 如果可以从任意陆地，通过只经过东西南北相邻的陆地，到达另一块陆地，则称日本列岛是连通的。随着地壳变动的进行，日本列岛可能变得连通。 给定初始时刻海域的情况，判断随着地壳变动反复进行，日本列岛是否会连通，并在可能连通时求出第一次连通需要多少次地壳变动。 ---

输入按以下格式从标准输入给出。 > $H$ $W$ $N$ $R_1$ $C_1$ $R_2$ $C_2$ $\dots$ $R_N$ $C_N$

请输出日本列岛第一次连通需要多少次地壳变动。如果初始就连通，输出 `0`。如果之后也永远无法连通，输出 `-1`。

## 子任务 1. （$5$ 分）$W = 1$。 2. （$9$ 分）$N = 2$。 3. （$8$ 分）$H \leq 500$，$W \leq 500$，$N \leq 500$。 4. （$28$ 分）$N \leq 2\,000$。 5. （$13$ 分）$H \times W \leq 200\,000$。 6. （$13$ 分）$H \times N \leq 200\,000$。 7. （$24$ 分）无额外限制。 --- ## 样例解释 1 下图是初始时刻海域的情况。黑色格子表示陆地，空白格子表示海洋。  第一次地壳变动后，新变为陆地的格子是 $(2,1)$、$(2,3)$、$(4,2)$、$(4,3)$ 共 $4$ 个。第一次变动后，依然无法仅通过东西南北相邻的陆地从 $(1,1)$ 走到 $(4,4)$，故此时日本列岛仍不连通。下图是第一次地壳变动后的海域情况。新增的斜线格子变为陆地，其他格子不变。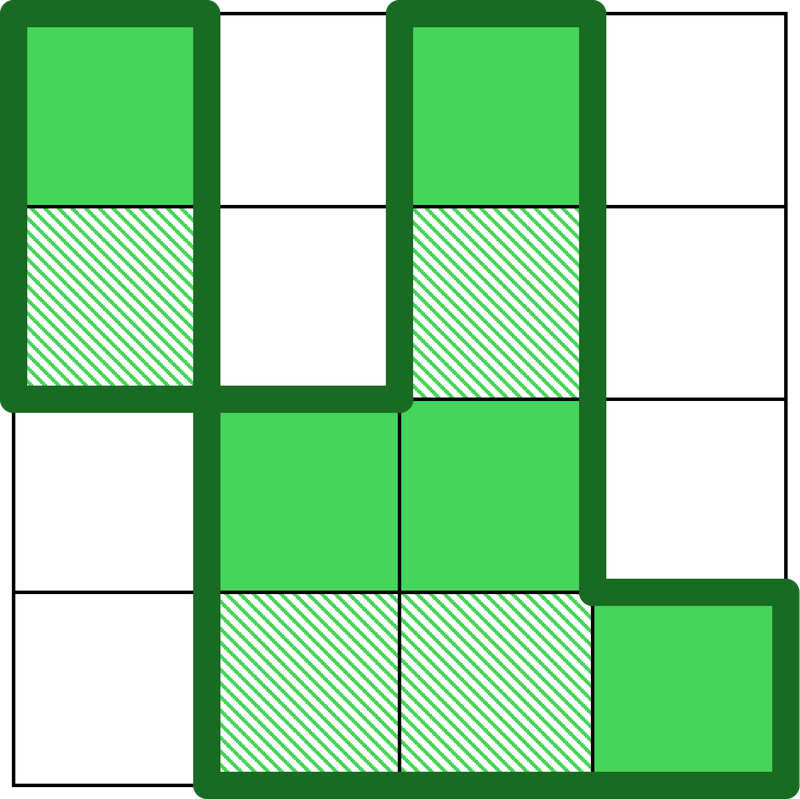  第二次地壳变动后，唯一新变为陆地的格子是 $(3,1)$。第二次变动后海域情况如下图。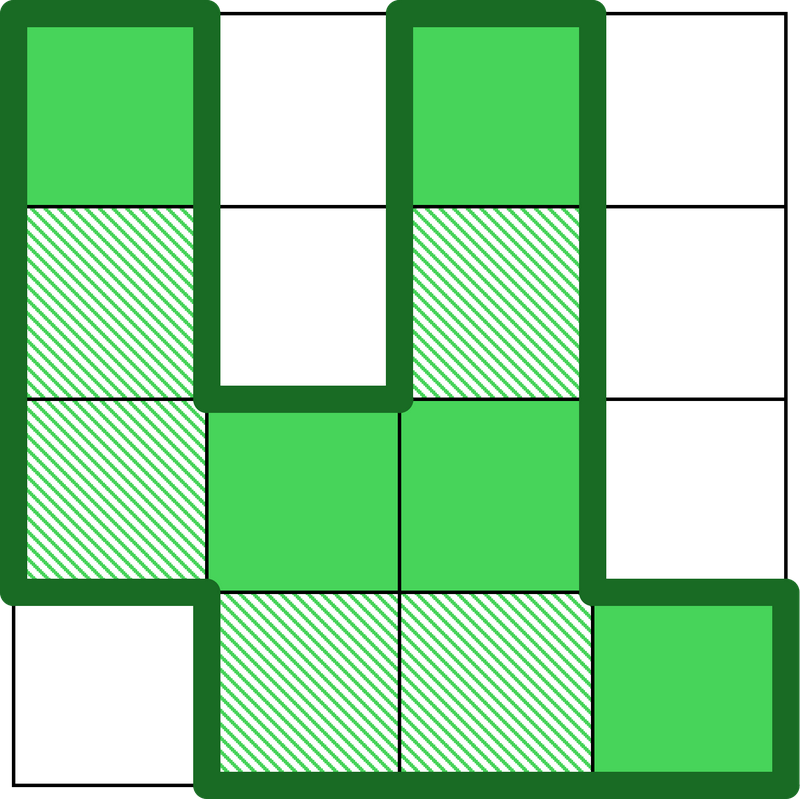  第二次地壳变动后日本列岛首次连通，输出 $2$。 该输入数据满足小任务 $3,4,5,6,7$ 的限制。 --- ## 样例解释 2 日本列岛不会连通，应输出 `-1`。 该输入数据满足小任务 $2,3,4,5,6,7$ 的限制。 --- ## 样例解释 3 日本列岛初始时即连通，输出 `0`。 该输入数据满足小任务 $2,3,4,5,6,7$ 的限制。 # 数据范围 - $1 \leq H \leq 200\,000$。 - $1 \leq W \leq 200\,000$。 - $2 \leq N \leq \min(H \times W,\ 200\,000)$。 - $1 \leq R_i \leq H\ (1 \leq i \leq N)$。 - $1 \leq C_i \leq W$。 - $(R_i, C_i) \neq (R_j, C_j)\ (1 \leq i < j \leq N)$。 - 输入数据均为整数。 由 ChatGPT 5 翻译