AT_joigsp2025_l 電子回路 2 (Circuit 2)
Description
N/A
Input Format
N/A
Output Format
N/A
Explanation/Hint
### 実装の詳細
あなたは $ 1 $ つのファイルを提出しなければならない.
あなたの提出するファイルは `circuit.cpp` という名前である. そのプログラムは `#include` プリプロセッサ指令によって `circuit.h` を読み込むこと.
`circuit.cpp` は以下の関数を実装していなければならない.
- `std::string solve(int N, int R, std::vector U, std::vector V)`
- この関数は各テストケースにおいて $ 1 $ 回だけ呼び出される.
- 引数 `N` は部品スロットの個数 $ N $ である.
- 引数 `R` は設置されている OR 部品の個数の上限 $ R $ である.
- 引数 `U`,`V` は長さ $ N $ の配列であり,`U[i]`,`V[i]` ( $ 0 \leqq i \leqq N - 1 $ ) は部品スロット $ i $ に接続されているスイッチの番号 $ U_{i}, V_{i} $ である.
- この関数は,以下の条件を満たす `&` と `|` からなる長さ $ N $ の文字列 $ t $ を返さなければならない.
- 各 $ i = 0, 1, \dots, N-1 $ について,部品スロット $ i $ に設置されている部品が AND 部品ならば `t[i]` は `&` であり,OR 部品ならば `t[i]` は `|` である.
- 戻り値 $ t $ の長さが $ N $ でない場合,**不正解\[1\]** と判定される.
- 戻り値 $ t $ に `&` でも `|` でもない文字が含まれる場合,**不正解\[2\]** と判定される.
- 実際に各部品スロットに設置されている部品の種類が,戻り値 $ t $ の表すものと異なる場合,**不正解\[3\]** と判定される.
あなたのプログラムは以下の関数を呼び出すことができる.
- `int query(std::string s)`
- あなたはこの関数を用いて JOI 君に質問をすることができる.
- 引数 `s` は `0` と `1` からなる長さ $ 2N + 1 $ の文字列でなければならない.各 $ j = 0, 1, \dots, 2N $ について,`s[j]` が `0` ならばスイッチ $ j $ を OFF にすることを,`s[j]` が `1` ならばスイッチ $ j $ を ON にすることを表す.
- 引数 `s` の長さが $ 2N+1 $ でない場合,**不正解\[4\]** と判定される.
- 引数 `s` に `0` でも `1` でもない文字が含まれる場合,**不正解\[5\]** と判定される.
- この関数を $ 1\,000 $ 回より多く呼び出してはならない. $ 1\,000 $ 回より多く呼び出した場合,**不正解\[6\]** と判定される.
- この関数の戻り値は,引数 `s` の通りにスイッチの状態を変更したときの回路ボードの出力である.
### 重要な注意
- 内部での使用のために他の関数を実装したり,グローバル変数を宣言するのは自由である.
- あなたの提出したプログラムは,標準入力・標準出力,あるいは他のファイルといかなる方法でもやりとりしてはならない.ただし,標準エラー出力にデバッグ情報等を出力することは許される.
### コンパイル・実行の方法
作成したプログラムをテストするための,採点プログラムのサンプルが, コンテストサイトからダウンロードできるアーカイブの中に含まれている. このアーカイブには,提出しなければならないファイルのサンプルも含まれている.
採点プログラムのサンプルは $ 1 $ つのファイルからなる. そのファイルは `grader.cpp` である. 作成したプログラムをテストするには, これらのファイル `grader.cpp`, `circuit.cpp`, `circuit.h` を同じディレクトリに置き,次のようにコマンドを実行する.
`g++ -std=gnu++20 -O2 -o grader grader.cpp circuit.cpp`
なお,アーカイブの中に含まれている `compile.sh` というファイルを代わりに実行してもよい.その場合,次のようにコマンドを実行する.
`./compile.sh`
コンパイルが成功すれば,`grader` という実行ファイルが生成される.
実際の採点プログラムは,採点プログラムのサンプルとは異なることに注意すること. 採点プログラムのサンプルは単一のプロセスとして起動する. このプログラムは,標準入力から入力を読み込み,標準出力に結果を出力する.
### 採点プログラムのサンプルの入力
$ T $ を関数 `solve` が返すべき長さ $ N $ の文字列とする.採点プログラムのサンプルは標準入力から以下の形式で入力を読み込む.
> $ N $ $ R $ $ U_0 $ $ V_0 $ $ U_1 $ $ V_1 $ $ \vdots $ $ U_{N-1} $ $ V_{N-1} $ $ T $
### 採点プログラムのサンプルの出力
採点プログラムのサンプルは標準出力へ以下の情報を出力する.
- 正解の場合,関数 `query` の呼び出し回数が `Accepted: 22` のように出力される.
- 不正解の場合,不正解の種類が `Wrong Answer [4]` のように出力される.
採点プログラムのサンプルは,いずれかの不正解の条件が満たされた時点で実行を終了する. 実行するプログラムが複数の不正解の条件を満たした場合,表示される不正解の種類はそれらのうち $ 1 $ つのみである.
### 採点に関する注意
実際の採点プログラムは適応的 (adaptive) ではなく,やりとりの初めから固定された答えを持つ.
### 小課題
1. ( $ 1 $ 点) $ N = 1 $ .
2. ( $ 8 $ 点) $ N \leqq 1\,000 $ , $ R = 1 $ .
3. ( $ 10 $ 点) $ N \leqq 1\,000 $ .
4. ( $ 21 $ 点) $ U_i = i + 1 $ , $ V_i = N + 1 + i $ ( $ 0 \leqq i \leqq N - 1 $ ), $ R \leqq 70 $ .
5. ( $ 9 $ 点) $ U_i = i + 1 $ , $ V_i = N + 1 + i $ ( $ 0 \leqq i \leqq N - 1 $ ).
6. ( $ 25 $ 点) $ U_i = 2i + 1 $ , $ V_i = 2i + 2 $ ( $ 0 \leqq i \leqq N - 1 $ ), $ R \leqq 70 $ .
7. ( $ 9 $ 点) $ U_i = 2i + 1 $ , $ V_i = 2i + 2 $ ( $ 0 \leqq i \leqq N - 1 $ ).
8. ( $ 14 $ 点) $ R \leqq 70 $ .
9. ( $ 3 $ 点) 追加の制約はない.
---
### やりとりの例
採点プログラムのサンプルが読み込む入力の例と,それに対応する関数の呼び出しの例を以下に示す.
### Sample Explanation 1

$ 1 $ 回目の `query` の呼び出しでは,回路ボードの出力は以下のように計算できる.
- スイッチ $ 1, 2 $ の状態はそれぞれ ON, OFF であるから,スイッチ $ 1, 2 $ はそれぞれ $ 1, 0 $ を出力する.
- 部品スロット $ 0 $ には OR 部品が設置されていて,接続するスイッチ $ 1, 2 $ はそれぞれ $ 1, 0 $ を出力しているから,部品スロット $ 0 $ は $ \max(1, 0) = 1 $ を出力する.
- スイッチ $ 0 $ の状態は OFF で,部品スロット $ 0 $ の出力は $ 1 $ であるから,スイッチ $ 0 $ の出力は $ 1 $ である.
- したがって,回路ボードの出力は $ 1 $ である.
この入力例はすべての小課題の制約を満たす.
---
### Sample Explanation 2
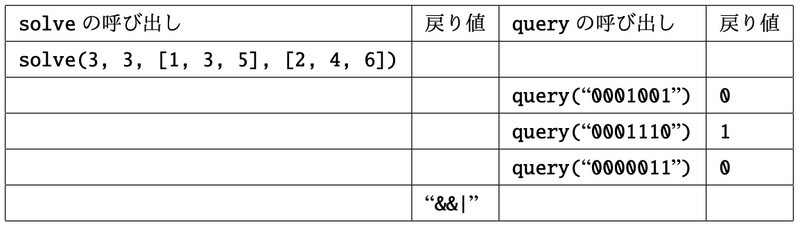
問題文中の図がこの入力例の回路ボードを表している.
この入力例は小課題 $ 3, 6, 7, 8, 9 $ の制約を満たす.
コンテストサイトからダウンロードできるファイルのうち,`sample-01-in.txt` は入力例 $ 1 $ に対応し,`sample-02-in.txt` は入力例 $ 2 $ に対応する. また,`sample-03-in.txt` は小課題 $ 3, 4, 5, 8, 9 $ の制約を満たし,`sample-04-in.txt` は小課題 $ 3, 6, 7, 8, 9 $ の制約を満たす.
### Constraints
- $ 1 \leqq N \leqq 8\,000 $ .
- $ 1 \leqq R \leqq \min(N, 120) $ .
- $ i < U_i < V_i \leqq 2N $ ( $ 0 \leqq i \leqq N - 1 $ ).
- $ j = 1, 2, \dots, 2N $ について, $ U_i = j $ または $ V_i = j $ であるような $ i $ ( $ 0 \leqq i \leqq N - 1 $ ) がただ $ 1 $ つ存在する.