AT_joisp2025_b 占い 3 (Fortune Telling 3)

Anna と Bruno は占いが好きでいつも二人で様々な占いをしている．今日は $ 0 $ か $ 1 $ が書かれたカードを使って $ Q $ 回の占いを行うことにした．この占いは二人が協力して行う必要があり， $ 1 $ 回の占いを行う具体的な方法は次のようなものである． 1. $ 0 $ か $ 1 $ が書かれたカードをたくさん用意し，シャッフルして山札にする． 2. Anna は山札からカードを $ 1 $ 枚ずつ，合計 $ N (=900) $ 枚引く．ここで，Anna と Bruno は $ N $ の値を知っている．Anna はカードを $ 1 $ 枚引く度にそのカードを捨てるか，場に出して並べるかを選択する． - 場に出して並べることを選択した場合は，すでに場に並べてあるカードの列の好きな位置に，今回並べるカードを挿入して並べる． - 具体的には，すでに場に $ l $ 枚のカードが並べてある場合，非負整数 $ x $ ( $ 0 \leqq x \leqq l $ ) を指定して，場に並べてあるカードの列の左から $ x $ 枚目のカードのすぐ右に挿入することができる．ただし $ x=0 $ のときはカードの列の一番左に挿入するとする． 3. Anna が $ N $ 枚のカードを引き終わると，Anna の役割は終了である．引いた $ N $ 枚のカードのうち $ 1 $ の書かれたカードの枚数が占いの結果である． 4. Bruno は最後に場に並べてあるカードの列のみを見て，占いの結果を推測する．Bruno が占いの結果を正しく答えることができれば占いは成功である． この占いにおいては，場に出すカードの枚数が少ないほど上手な占いであるとされる．Anna と Bruno が $ Q $ 回の占いを成功させるための戦略を実装したプログラムを作成せよ．この課題では，Anna が場に出すカードの枚数が少ないほど，あなたは高得点を得る．

N/A

N/A

### 実装の詳細 あなたは $ 2 $ つのファイルを提出しなければならない． $ 1 $ つ目のファイルは `Anna.cpp` という名前である．このファイルは Anna の戦略を実装したファイルであり，以下の関数を実装していなければならない．また，`#include` プリプロセッサ指令によって `Anna.h` を読み込むこと． - `void Anna(int N)` この関数は，合計 $ Q $ 回呼び出される． $ i $ 回目 ( $ 1 \leqq i \leqq Q $ ) の呼び出しは， $ i $ 回目の占いにおける Anna の手順に相当する． - 引数 `N` は，Anna が山札からカードを引く枚数 $ N $ である． 関数 Anna の $ 1 $ 回の呼び出しについて，以下の関数を $ N+1 $ 回呼び出さなければならない． - `int DrawCard(int x)` この関数を用いて，山札からカードを引き，そのカードを捨てるか，場に出して並べるかを選択する． $ j $ 回目 ( $ 1 \leqq j \leqq N $ ) の呼び出しの戻り値で， $ j $ 枚目に引いたカードに書かれた数を受け取る． $ k $ 回目 ( $ 2 \leqq k \leqq N+1 $ ) の呼び出しの引数で $ k-1 $ 枚目に引いたカードに対する操作を指定する． - $ j $ 回目 ( $ 1\leqq j \leqq N $ ) の呼び出しにおける戻り値は $ 0 $ または $ 1 $ であり，Annaが $ j $ 枚目に引いたカードに書かれた数を表す． - $ N+1 $ 回目の呼び出しにおける戻り値は $ -1 $ であり，Annaが $ N $ 枚のカードを引き終えたことを表す． - **$ 1 $ 回目の呼び出しにおける引数 $ x $ は $ x=-1 $ を満たさなければならない**．これが満たされない場合 **不正解 \[1\]** と判定される． - $ k $ 回目 ( $ 2\leqq k \leqq N+1 $ ) の呼び出しにおける引数 $ x $ は $ k-1 $ 枚目に引いたカードに対する操作を指定する． $ x=-1 $ のとき， $ k-1 $ 枚目に引いたカードを捨てることを表す． $ 0\leqq x $ のとき， $ k-1 $ 枚目に引いたカードをすでに場にあるカードの列の左から $ x $ 枚目のカードのすぐ右に挿入することを表す．ただし $ x=0 $ のときはカードの列の一番左に挿入することを表す．ここで，すでに場にあるカードの枚数を $ l $ として $ -1 \leqq x \leqq l $ を満たさなければならない．これが満たされない場合，**不正解 \[2\]** と判定される． - 関数 `Anna` の実行の終了時に関数 `DrawCard` の呼び出し回数が $ N+1 $ 回でなかった場合，**不正解 \[3\]** と判定される． $ 2 $ つ目のファイルは `Bruno.cpp` という名前である． このファイルは Bruno の戦略を実装したファイルであり，以下の関数を実装していなければならない． また，`#include` プリプロセッサ指令によって `Bruno.h` を読み込むこと． - `int Bruno(int N, int L, std::vector C)` この関数は，Anna が一連の占いの手順を終える度に $ 1 $ 回，合計で $ Q $ 回呼び出される． $ i $ 回目 ( $ 1 \leqq i \leqq Q $ ) の呼び出しは， $ i $ 回目の占いにおける Bruno の手順に相当する．Anna が山札から引いた $ 1 $ の書かれたカードの枚数を戻り値として返さなければならない． - 引数 `N` は Anna が山札からカードを引いた枚数 $ N $ である． - 引数 `L` は場に並べられたカードの枚数 $ L $ である． - 引数 `C` は，長さ $ L $ の配列であり，`C[l-1]` は場の左から $ l $ 番目 ( $ 1 \leqq l \leqq L $ ) に並べられたカードに書かれた数を表す． - 関数 `Bruno` の戻り値が Anna が山札から引いた $ 1 $ の書かれたカードの枚数と異なる場合，**不正解 \[4\]** と判定される． #### 重要な注意 - 内部での使用のために他の関数を実装したり，グローバル変数を宣言するのは自由である．ただし，提出された $ 2 $ つのプログラムは，採点プログラムとまとめてリンクされて $ 1 $ つの実行ファイルになるので，各ファイル内のすべてのグローバル変数と内部関数を無名名前空間内で宣言して，他のファイルとの干渉を避ける必要がある．採点時には，このプログラムは Anna 側，Bruno 側として $ 2 $ 個のプロセスとして実行されるので，Anna 側と Bruno 側でプログラム中のグローバル変数を共有することはできない． - あなたの提出したプログラムは，標準入力・標準出力，あるいは他のファイルといかなる方法でもやりとりしてはならない．ただし，標準エラー出力にデバッグ情報等を出力することは許される． ### コンパイル・実行の方法 作成したプログラムをテストするための，採点プログラムのサンプルが，コンテストサイトからダウンロードできるアーカイブの中に含まれている．このアーカイブには，提出しなければならないファイルのサンプルも含まれている． 採点プログラムのサンプルは $ 1 $ つのファイルからなる．そのファイルは `grader.cpp` である．作成したプログラムをテストするには，`grader.cpp`，`Anna.cpp`，`Bruno.cpp`，`Anna.h`，`Bruno.h` を同じディレクトリに置き，次のようにコマンドを実行する． `g++ -std=gnu++20 -O2 -o grader grader.cpp Anna.cpp Bruno.cpp` なお，アーカイブの中に含まれている `compile.sh` というファイルを代わりに実行してもよい．その場合，次のようにコマンドを実行する． `./compile.sh` コンパイルが成功すれば，`grader` という実行ファイルが生成される． 実際の採点プログラムは，採点プログラムのサンプルとは異なることに注意すること．採点プログラムのサンプルは単一のプロセスとして起動する．このプログラムは，標準入力から入力を読み込み，標準出力に結果を出力する． ### 採点プログラムのサンプルの入力 採点プログラムのサンプルは標準入力から以下の形式で入力を読み込む． > $ Q $ $ N $ $ A_{1,1} $ $ A_{1,2} $ $ \cdots $ $ A_{1,N} $ $ A_{2,1} $ $ A_{2,2} $ $ \cdots $ $ A_{2,N} $ $ \vdots $ $ A_{Q,1} $ $ A_{Q,2} $ $ \cdots $ $ A_{Q,N} $ $ A_{i,j} $ ( $ 1 \leqq i \leqq Q, 1 \leqq j \leqq N $ ) は Anna が $ i $ 回目の占いで $ j $ 枚目に引くカードに書かれた数を表す． ### 採点プログラムのサンプルの出力 採点プログラムのサンプルは標準出力へ以下の情報を出力する(引用符は実際には出力されない)． - 正解の場合，すべての占いにおける Anna が場に出したカードの枚数 $ L $ の最大値が `Accepted: 100` のように出力される． - 不正解の場合，不正解の種類が `Wrong Answer [1]` のように出力される． 実行するプログラムが複数の不正解の条件を満たした場合， 表示される不正解の種類はそれらのうち $ 1 $ つのみである． 採点プログラムのサンプルは，不正解の条件を満たした場合，途中で実行を打ち切ることがある． ### 採点に関する注意 すべてのテストケースについて，実際の採点プログラムは適応的 (adaptive) **ではない**．これは，採点プログラムは初めから固定された山札から引くカードの列を持つということを意味する． --- ### 採点基準 この課題のテストケースの中で， $ 1 $ つでも**不正解 \[1\] ～ \[4\]** (実装の詳細を参照) と判定されたものや， 実行時間制限超過，メモリ制限超過，実行時エラーと判定されたものがあった場合， $ 0 $ 点となる． またこの課題におけるすべてのテストケースに正解した場合，この課題のすべてのテストケースで， 関数 Anna の $ 1 $ 回の呼び出しについて引数 $ 0 \leqq x $ で関数 `DrawCard` を呼び出した回数の最大値を $ L $ として，以下のように採点される． - $ 500 < L $ のとき， $ 3 $ 点 - $ 14 < L \leqq 500 $ のとき， $ \left\lfloor 100 \times \left(\dfrac{2.5}{L-11.5}\right)^{0.35} \right\rfloor $ 点 - $ L \leqq 14 $ のとき， $ 100 $ 点 ### やり取りの例 採点プログラムのサンプルが読み込む入力の例と，それに対応する関数の呼び出しの例を以下に示す． ### Sample Explanation 1  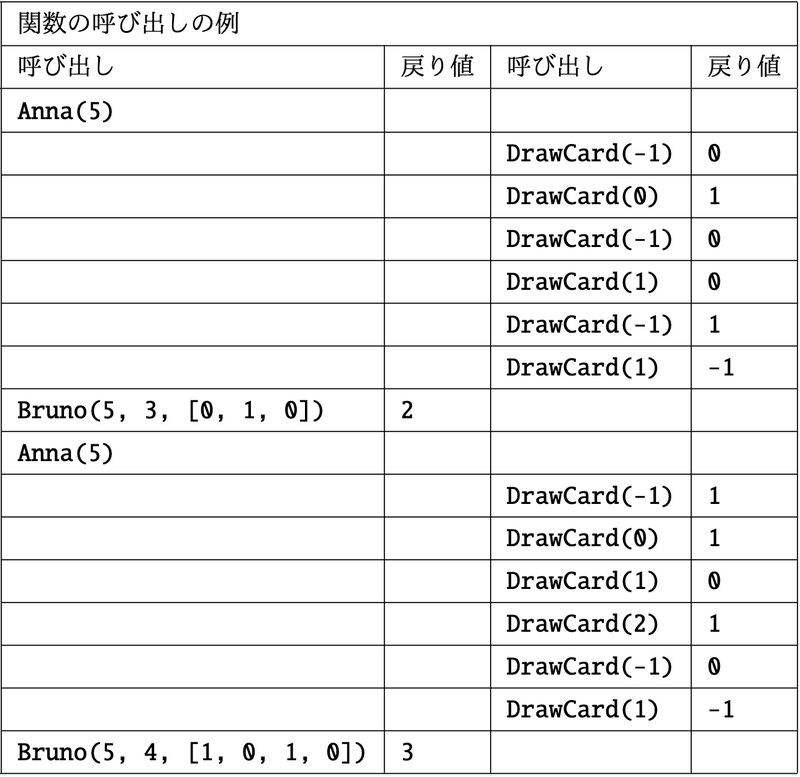この入力例は $ Q (=2) $ 回の占いからなり， $ 2 $ 回の占いでAnnaが山札から引くカードの枚数は $ N (=5) $ 枚である． この例では， $ 1 $ 回目の占いは Anna は次のような手順で占いを行う． 1. Anna が山札からカードを $ 1 $ 枚引く．引いたカードに書かれた数は $ 0 $ である． 2. Anna は引いたカードを場に出して並べることを選択し，場に並べてあるカードの列の一番左に挿入する．場に並べられたカードの列は $ 0 $ になる．Anna は山札からカードを $ 1 $ 枚引く，引いたカードに書かれた数は $ 1 $ である． 3. Anna は引いたカードを捨てることを選択する．Anna は山札からカードを $ 1 $ 枚引く，引いたカードに書かれた数は $ 0 $ である． 4. Anna は引いたカードを場に出して並べることを選択し，場に並べてあるカードの列の左から $ 1 $ 枚目のカードのすぐ右に挿入する．場に並べられたカードの列は $ 0,0 $ になる．Anna は山札からカードを $ 1 $ 枚引く，引いたカードに書かれた数は $ 0 $ である． 5. Anna は引いたカードを捨てることを選択する．Anna は山札からカードを $ 1 $ 枚引く，引いたカードに書かれた数は $ 1 $ である． 6. Anna は引いたカードを場に出して並べることを選択し，場に並べてあるカードの列の左から $ 1 $ 枚目のカードのすぐ右に挿入する．場に並べられたカードの列は $ 0,1,0 $ になる． Bruno は $ N $ の値と場に並べられたカードの列 $ 0,1,0 $ をもとに，Anna が引いた $ 1 $ の書かれたカードの枚数が $ 2 $ であると答える． これは正しいため，占いは成功である．1回目の占いで Anna が場に出したカードの枚数 $ L $ は $ 3 $ である． $ 2 $ 回目の占いで Anna が場に出したカードの枚数 $ L $ は $ 4 $ である． この入力例は**制約を満たさない**ことに注意すること． コンテストサイトからダウンロードできるファイルのうち，`sample-01-in.txt` は入力例 $ 1 $ に対応する． コンテストサイトからダウンロードできるファイルのうち，`sample-02-in.txt` は制約を満たす． ### Constraints すべての入力データは以下の条件を満たす． - $ 1 \leqq Q \leqq 100 $ ． - $ N = 900 $ ． - $ A_{i,j} $ は $ 0 $ または $ 1 $ である ( $ 1 \leqq i \leqq Q, 1 \leqq j \leqq N $ )．