AT_kupc2024_g Genjikou
题目描述
给定正整数 $N, A, B$。
将集合 $\lbrace 1,\ldots,N \rbrace$ 分成若干个(至少一个)互不相交且不区分顺序的子集 $\lbrace S_1,\ldots,S_K \rbrace$,称之为一次分割。例如,$\lbrace 1,2,3,4 \rbrace$ 的分割 $\lbrace \lbrace 1,3 \rbrace, \lbrace 2,4 \rbrace \rbrace$ 与 $\lbrace \lbrace 2,4 \rbrace, \lbrace 1,3 \rbrace \rbrace$ 视为同一种分割。
对于每种分割 $\lbrace S_1,\ldots,S_K \rbrace$ 以及一组互不相同的正整数 $\lbrace H_1,\ldots,H_K \rbrace$,定义**源氏香之图**如下:
- 对每个 $1 \le i \le K$,在二维平面上为 $S_i$ 画出 $2|S_i|-1$ 条线段,这被称为源氏香之图。
- 对于 $x \in S_i$,连接 $(x,0)$ 与 $(x,H_i)$。
- 对于每个 $1 \le j \le |S_i|-1$,连接 $(S_{i,j},H_i)$ 与 $(S_{i,j+1},H_i)$,其中 $S_{i,j}$ 表示 $S_i$ 内按大小排序的第 $j$ 大的整数。
此外,满足如下条件的分割被称为**好分割**:
- 对于任意一组互不相同的正整数 $\lbrace H_1,\ldots,H_K \rbrace$,在源氏香之图中,只通过已画的线段,所有点 $(x,0)$($1 \le x \le N$)都是连通的。
对于 $\lbrace 1,\ldots,N \rbrace$ 的所有分割 $\lbrace S_1,\ldots,S_K \rbrace$,且每个子集 $S_i$ 的元素个数满足 $A \le |S_i| \le B$,请计算好分割的种数,并输出其对 $998244353$ 取模的结果。
输入格式
输入为一行,包含三个整数。
> $N\ A\ B$
输出格式
输出答案。
说明/提示
### 样例解释 1
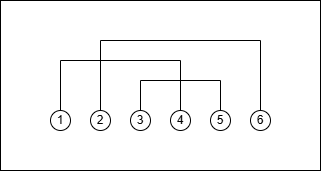
如图所示,$\lbrace \lbrace 1,4 \rbrace, \lbrace 2,6 \rbrace, \lbrace 3,5 \rbrace \rbrace$ 是一个好分割。其对应的源氏香之图可以如下绘制,注意所有通过线段的交点也视为已连接,故此满足连通性。
### 样例解释 2
请输出答案模 $998244353$ 的结果。
### 数据范围
- 所有输入均为整数
- $1 \le A \le B \le N \le 10^5$
由 ChatGPT 5 翻译