AT_kupc2024_g Genjikou

正整数 $ N,A,B $ が与えられます。 $ \lbrace 1,\ldots,N \rbrace $ を区別のない $ 1 $ つ以上のグループに分けた族 $ \lbrace S_1,\ldots,S_K \rbrace $ を分割と呼びます。例えば、 $ \lbrace 1,2,3,4 \rbrace $ の分割 $ \lbrace \lbrace 1,3 \rbrace,\lbrace 2,4 \rbrace \rbrace,\lbrace \lbrace 2,4 \rbrace,\lbrace 1,3 \rbrace \rbrace $ は同じ分割とみなします。 分割 $ \lbrace S_1,\ldots,S_K \rbrace $ と相異なる正整数の組 $ \lbrace H_1,\ldots,H_K \rbrace $ について、**源氏香の図**を以下のように定義します。 - 各 $ 1 \le i \le K $ について $ S_i $ に対応する $ 2|S_i|-1 $ 本の線分を $ 2 $ 次元平面上に描き、これを源氏香の図と呼ぶ。 - $ x \in S_i $ について、 $ (x,0),(x,H_i) $ 間を結ぶ。 - 各 $ 1 \le j \le |S_i|-1 $ について、 $ (S_{i,j},H_i),(S_{i,j+1},H_i) $ 間を結ぶ。ここで、 $ S_{i,j} $ は $ S_i $ に含まれる $ j $ 番目に大きい整数。 また、次の条件を満たす分割を**良い分割**と呼びます。 - 任意の相異なる正整数の組 $ \lbrace H_1,\ldots,H_K \rbrace $ に対する源氏香の図について、描いた線分のみを通って各 $ 1 \le x \le N $ の点 $ (x,0) $ が全て連結になる。 $ \lbrace 1,\ldots,N \rbrace $ の分割 $ \lbrace S_1,\ldots,S_K \rbrace $ であって各部分集合 $ S_i $ の個数が $ A $ 以上 $ B $ 以下であるもののうち、良い分割であるものの個数を $ 998244353 $ で割った余りを求めてください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ A $ $ B $

答えを出力せよ。

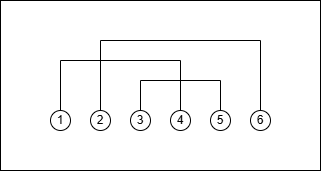
### Sample Explanation 1 良い分割の例として $ \lbrace \lbrace 1,4 \rbrace,\lbrace 2,6 \rbrace,\lbrace 3,5 \rbrace \rbrace $ が挙げられます。あり得る源氏香の図として以下の形があり、線分の交点も接続されていることに注意するとこれは連結になっています。  ### Sample Explanation 2 答えを $ 998244353 $ で割った余りを出力してください。 ### Constraints - 入力は全て整数 - $ 1 \le A \le B \le N \le 10^5 $