AT_masters2025_final_a Cooperative Trash Sorting (A)

第二回マスターズ選手権のオンサイト決勝大会が終了した。 大会会場には燃えるごみ、燃えないごみ、資源ごみの3種類のごみが散乱している。 高橋くんは燃えるごみを、青木くんは燃えないごみを、それぞれ担当して回収することになった。 2人はごみ袋を両手に広げ、会場内を歩き回りながらごみを回収していく。 ごみは正しく分別する必要があり、高橋くんは燃えるごみのみを、青木くんは燃えないごみのみを回収したい。 資源ごみは後で業者が回収するため、その場に残しておく。 できるだけ短い時間で、燃えるごみと燃えないごみをすべて回収してほしい。

$ 10^6\times 10^6 $ の二次元平面上に、点として表される $ X $ 個の燃えるごみ、 $ Y $ 個の燃えないごみ、 $ Z $ 個の資源ごみが散乱している。 あなたは高橋くんと青木くんに指示を出し、それぞれすべての燃えるごみ・燃えないごみを回収させたい。 高橋くんと青木くんは、それぞれごみ袋の端を左右の手で持っており、ごみ袋の開口部は左右の手を結ぶ線分として表される。 左手の現在位置を $ p=(p_x, p_y) $ 、右手の現在位置を $ q=(q_x, q_y) $ とし、1回の操作でそれぞれを $ p'=(p_x', p_y') $ および $ q'=(q_x', q_y') $ に直線的に移動させる。 このとき、2つの三角形 $ \triangle pqp' $ および $ \triangle p'qq' $ の内部およびその境界上にあるごみは、**すべて**回収され、平面上から取り除かれる。 この操作を繰り返すことで、ごみ袋を操作してごみを回収する。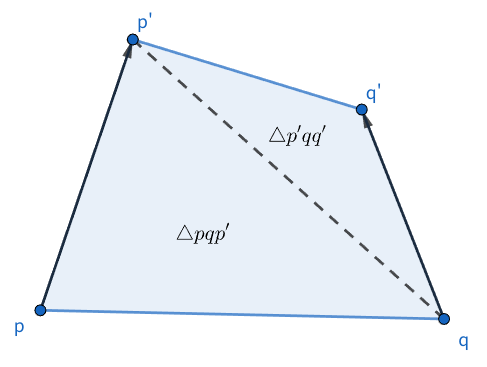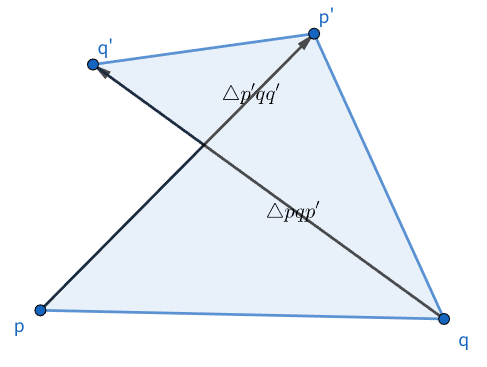   注意: 左右の手の動きが交差する場合に回収する領域が直感と異なるように見えるかもしれないが、この問題では簡単のため左手を先に動かしてから次に右手を動かしたものとして扱っている。 高橋くんと青木くんの計4本の手は同じ座標に重なってもかまわない。 両方の手を重ねて一緒に動かす場合など、三角形が線分に退化している場合、線分上のごみが回収される。 ヒント: 三角形に対する点の内外判定 三角形 $ \triangle abc $ の内部またはその境界上に、点 $ p $ が存在するかどうかは、たとえば以下の Python コードにより判定することができる。 ここでは、 $ p[0] $ が $ x $ 座標、 $ p[1] $ が $ y $ 座標を表す。 このコードは、三角形が線分や1点に退化している場合でも正しく動作し、さらにすべて整数演算で処理されるため、誤差なく判定が可能である。 ``` def orient(a, b, p): return (b[0] - a[0]) * (p[1] - a[1]) - (b[1] - a[1]) * (p[0] - a[0]) def contains(p, a, b, c): # degenerate (colinear) case if orient(a, b, c) == 0: if orient(a, b, p) != 0 or orient(a, c, p) != 0: return False xs = (a[0], b[0], c[0]) ys = (a[1], b[1], c[1]) return min(xs)

入力は以下の形式で標準入力から与えられる。 > $ X $ $ Y $ $ Z $ $ x_0 $ $ y_0 $ $ \vdots $ $ x_{X+Y+Z-1} $ $ y_{X+Y+Z-1} $ - 燃えるごみの個数 $ X $ は $ X=100 $ で固定されている。 - 燃えないごみの個数 $ Y $ は $ Y = 0 $ または $ Y = 100 $ のいずれかである。 - 資源ごみの個数 $ Z $ は $ 0\leq Z\leq 100 $ を満たす。 - ごみの座標は整数 $ (x_i, y_i) $ で与えられ、すべての座標は $ 1 \leq x_i, y_i \leq 10^6 - 1 $ を満たす。 - ごみの種別とインデックスの対応は次の通り： - $ i = 0, \dots, X - 1 $ ：燃えるごみ - $ i = X, \dots, X + Y - 1 $ ：燃えないごみ - $ i = X + Y, \dots, X + Y + Z - 1 $ ：資源ごみ - 任意の2つのごみの間のユークリッド距離は、 $ 10^3 $ 以上離れていることが保証される。 - 以下の4つの条件のそれぞれを満たすような燃えるごみ $ (x,y) $ が、少なくとも1つずつ存在する。これにより、燃えるごみをすべて回収するには、少なくとも $ T\geq 2\times 10^5 $ の時間が必要なことが保証される。 - $ x\leq 4\times 10^5 $ かつ $ y\leq 4\times 10^5 $ - $ x\leq 4\times 10^5 $ かつ $ y\geq 6\times 10^5 $ - $ x\geq 6\times 10^5 $ かつ $ y\leq 4\times 10^5 $ - $ x\geq 6\times 10^5 $ かつ $ y\geq 6\times 10^5 $

高橋くんの左右の手の初期位置をそれぞれ $ (x_{0,0},y_{0,0}) $ 、 $ (x_{0,1},y_{0,1}) $ 、青木くんの左右の手の初期位置をそれぞれ $ (x_{0,2},y_{0,2}) $ 、 $ (x_{0,3},y_{0,3}) $ とする。 操作回数を $ K $ とし、 $ t $ 回目の操作 ( $ t=1,2,\cdots, K $ ) では、高橋くんの左右の手の移動先を $ (x_{t,0},y_{t,0}) $ 、 $ (x_{t,1},y_{t,1}) $ 、青木くんの左右の手の移動先を $ (x_{t,2},y_{t,2}) $ 、 $ (x_{t,3},y_{t,3}) $ とする。 このとき、以下の形式で標準出力に出力せよ。 > $ x_{0,0} $ $ y_{0,0} $ $ x_{0,1} $ $ y_{0,1} $ $ x_{0,2} $ $ y_{0,2} $ $ x_{0,3} $ $ y_{0,3} $ $ \vdots $ $ x_{K,0} $ $ y_{K,0} $ $ x_{K,1} $ $ y_{K,1} $ $ x_{K,2} $ $ y_{K,2} $ $ x_{K,3} $ $ y_{K,3} $ なお、入力によっては燃えないごみが存在せず、青木くんの作業が不要な場合がある。 その場合には、たとえば $ x_{t,2}=y_{t,2}=x_{t,3}=y_{t,3}=0 $ と出力し、青木くんを隅で待機させておけば良い。

### 得点 高橋くんが回収した燃えるごみの個数を $ X' $ 、青木くんが回収した燃えないごみの個数を $ Y' $ 、回収されなかった資源ごみの個数を $ Z' $ とする。 合計時間を $ T $ としたとき、以下の得点が得られる。 - $ X'+Y'+Z'=X+Y+Z $ かつ $ T\leq 10^8 $ の場合、 $ \mathrm{round}\left(10^6\times \left(1+\log_2 \frac{10^8}{T}\right)\right) $ - $ X'+Y'+Z'\lt X+Y+Z $ もしくは $ T>10^8 $ の場合、 $ \mathrm{round}\left(10^6\times \frac{X'+Y'+Z'}{X+Y+Z}\right) $ 入力生成方法の違いにより、問題は A・B・C の 3 問 に分かれている。 各問題にはそれぞれ 150 個のテストケース があり、各テストケースの得点の合計がその問題に対する提出の得点となる。 一つ以上のテストケースで不正な出力や制限時間超過をした場合、提出全体の判定がWAやTLEとなる。 各問題に対して獲得した最高得点の総和で最終順位が決定され、コンテスト終了後のシステムテストは行われない。 同じ得点を複数のチームが得た場合、提出時刻に関わらず同じ順位となる。 ### 入力生成方法 - $ \mathrm{rand}(L,U) $ : $ L $ 以上 $ U $ 以下の整数値を一様ランダムに生成する。 - $ \mathrm{rand\_double}(L,U) $ : $ L $ 以上 $ U $ 以下の実数値を一様ランダムに生成する。 - $ \mathrm{normal}(\sigma) $ : 平均 $ 0 $ 、標準偏差 $ \sigma $ の正規分布からランダムに実数値を生成する。 各問題における、燃えないごみの個数 $ Y $ および資源ごみの個数 $ Z $ の範囲は、以下の表の通りである。 問題 Y Z A 0 $ 10 $ から $ 100 $ B $ 100 $ $ 0 $ C $ 100 $ $ 1 $ から $ 100 $ ごみは、燃えるごみ → 燃えないごみ → 資源ごみ の順に、各種類について以下の手順で座標を生成する。 1. ごみの個数 $ N $ を、指定範囲内から一様ランダムに決定する。 2. クラスタ数 $ n $ を、 $ \mathrm{rand}(5,10) $ により決定する。 3. 各クラスタ $ i = 1, \dots, n $ に対し、以下のパラメータを生成する： - 重み $ w_i=\mathrm{rand\_double}(0,1) $ - 中心座標 $ cx_i,cy_i=\mathrm{rand}(200000,800000) $ - 標準偏差 $ \sigma_{x,i},\sigma_{y,i}=\mathrm{rand}(30000,90000) $ - 傾き $ \theta_i=\mathrm{rand\_double}(0,\pi) $ 4. 以下の処理を $ N $ 回繰り返して、ごみの座標 $ (x, y) $ を $ N $ 個生成する： - 重みに比例した確率でクラスタ $ i $ を選ぶ。 - $ x' = \mathrm{normal}(\sigma_{x,i}) $ 、 $ y' = \mathrm{normal}(\sigma_{y,i}) $ を生成する。 - 座標 $ (x, y) $ を以下の式で計算する： \\\[ x=\\mathrm{round}(cx\_i+\\cos(\\theta\_i)\\cdot x'-\\sin(\\theta\_i)\\cdot y')\\\\ y=\\mathrm{round}(cy\_i+\\sin(\\theta\_i)\\cdot x'+\\cos(\\theta\_i)\\cdot y') \\\] - $ (x, y) $ が $ 1 \leq x, y \leq 10^6 - 1 $ を満たし、かつこれまでに生成されたどのごみともユークリッド距離が $ 10^3 $ 以上離れている場合、その座標を採用する。条件を満たさない場合は座標の再生成を行う。 ごみの種類が「燃えるごみ」の場合には、以下の4つの領域それぞれに該当するごみが少なくとも1つずつ存在することを確認する： - $ x\leq 4\times 10^5 $ かつ $ y\leq 4\times 10^5 $ - $ x\leq 4\times 10^5 $ かつ $ y\geq 6\times 10^5 $ - $ x\geq 6\times 10^5 $ かつ $ y\leq 4\times 10^5 $ - $ x\geq 6\times 10^5 $ かつ $ y\geq 6\times 10^5 $ 存在しない場合、クラスタ数の生成のステップからやり直す。 ### C問題について **C問題の入力は、各チームが自ら作成して提出によって差し替えることができる。** 作成した入力の提出方法については、D問題のページを参照せよ。 各チームは4つの入力を提出する。提出された4つの入力のうち、ランダムに1件が全チームに公開され、残りの3件がジャッジに使用される。 **入力の公開およびジャッジの開始は、コンテスト開始から3時間30分後を目安としている。** 準備が整い次第、全体アナウンスを行う。 入力を提出しなかったチームの分は、前述の入力生成方法に従ってランダムに生成された4つの入力が代わりに用いられる。 なお、自分のチームが提出した入力は既知であるため、対応する出力を事前に計算して解答プログラムに埋め込むことも許される。 D問題への提出は何度でも行うことができる。ただし、各チームについて、コンテスト開始から **180 分未満** に提出されたもので ACを獲得した提出のうち、最後の1件のみが使用される。 ### ツール(入力ジェネレータ・スコア計算) - [ローカル版](https://img.atcoder.jp/masters2025-final/ACwJzml3.zip): 使用するには[Rust言語](https://www.rust-lang.org/ja)のコンパイル環境をご用意下さい。 - [Windows用のコンパイル済みバイナリ](https://img.atcoder.jp/masters2025-final/ACwJzml3_windows.zip): Rust言語の環境構築が面倒な方は代わりにこちらをご利用下さい。 コンテスト期間中に、チーム外とのビジュアライズ結果の共有や解法・考察に関する言及は禁止されています。ご注意下さい。