AT_masters2025_final_a Cooperative Trash Sorting (A)

The on-site finals of the 2nd Masters Championship have just concluded. At the venue, three types of trash—burnable trash, non-burnable trash, and recyclable trash—are scattered across the floor. Takahashi is assigned to collect burnable trash, and Aoki is assigned to collect non-burnable trash. Each of them holds a trash bag open with both hands and walks around the venue to collect trash. Proper sorting of trash is required: Takahashi should collect only burnable trash, and Aoki should collect only non-burnable trash. Recyclable trash will be collected later by a professional service, so it should be left in place. Your task is to help them collect all burnable and non-burnable trash in as little time as possible.

On a two-dimensional plane of size $ 10^6 \times 10^6 $ , there are $ X $ burnable trash items, $ Y $ non-burnable trash items, and $ Z $ recyclable trash items, each represented as a point. You are to instruct Takahashi and Aoki so that they collect all burnable and non-burnable trash respectively. Takahashi and Aoki each hold the ends of a trash bag with their left and right hands, and the opening of the bag is represented by a line segment connecting their two hands. Let the current positions of the left and right hands be $ p = (p_x, p_y) $ and $ q = (q_x, q_y) $ , respectively. In one operation, the hands can be moved in a straight line to new positions $ p' = (p_x', p_y') $ and $ q' = (q_x', q_y') $ . At this time, **all** trash located on or inside the two triangles $ \triangle pqp' $ and $ \triangle p'qq' $ is collected and removed from the plane. By repeating this operation, the trash bag can be moved to collect trash.   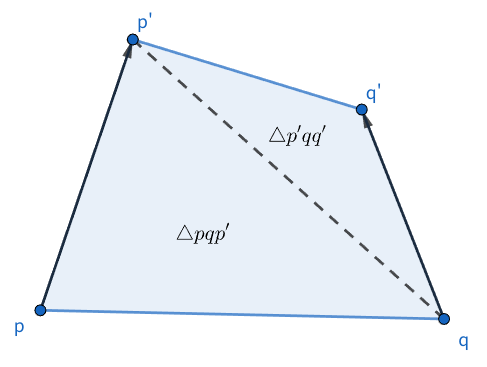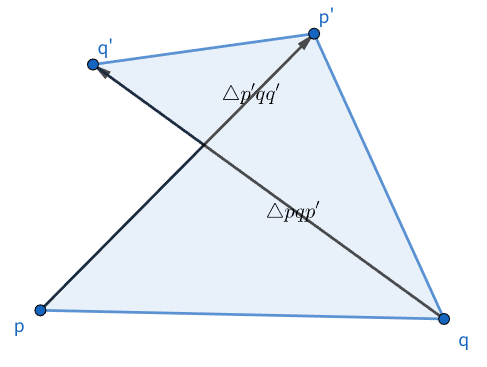Note: When the movements of the left and right hands cross over, the collected area may appear counterintuitive. However, in this problem, for simplicity, the operation is treated as if the left hand moves first, followed by the right hand. The four hands of Takahashi and Aoki are allowed to overlap at the same coordinates. When the triangle degenerates into a line segment, such as when both hands move together along the same path, trash located on the line segment is collected. Hint: Point-in-triangle test Whether a point $ p $ lies inside or on the boundary of a triangle $ \triangle abc $ can be determined using the following Python code as an example. Here, $ p[0] $ and $ p[1] $ represent the $ x $ - and $ y $ -coordinates of the point $ p $ , respectively. This code works correctly even when the triangle degenerates into a line segment or a single point, and since it uses only integer arithmetic, it allows for exact evaluation without rounding errors. ``` def orient(a, b, p): return (b[0] - a[0]) * (p[1] - a[1]) - (b[1] - a[1]) * (p[0] - a[0]) def contains(p, a, b, c): # degenerate (colinear) case if orient(a, b, c) == 0: if orient(a, b, p) != 0 or orient(a, c, p) != 0: return False xs = (a[0], b[0], c[0]) ys = (a[1], b[1], c[1]) return min(xs)

Input is given from Standard Input in the following format: > $ X $ $ Y $ $ Z $ $ x_0 $ $ y_0 $ $ \vdots $ $ x_{X+Y+Z-1} $ $ y_{X+Y+Z-1} $ - The number of burnable trash items $ X $ is fixed at $ X = 100 $ . - The number of non-burnable trash items $ Y $ is either $ Y = 0 $ or $ Y = 100 $ . - The number of recyclable trash items $ Z $ satisfies $ 0 \leq Z \leq 100 $ . - Trash coordinates are given as integer pairs $ (x_i, y_i) $ , where all values satisfy $ 1 \leq x_i, y_i \leq 10^6 - 1 $ . - The correspondence between index $ i $ and trash type is as follows: - $ i = 0, \dots, X - 1 $ : burnable trash - $ i = X, \dots, X + Y - 1 $ : non-burnable trash - $ i = X + Y, \dots, X + Y + Z - 1 $ : recyclable trash - The Euclidean distance between any two trash items is guaranteed to be at least $ 10^3 $ . - For each of the following four conditions, there exists at least one burnable trash item $ (x, y) $ that satisfies it. This ensures that collecting all burnable trash requires at least $ T \geq 2 \times 10^5 $ time. - $ x \leq 4 \times 10^5 $ and $ y \leq 4 \times 10^5 $ - $ x \leq 4 \times 10^5 $ and $ y \geq 6 \times 10^5 $ - $ x \geq 6 \times 10^5 $ and $ y \leq 4 \times 10^5 $ - $ x \geq 6 \times 10^5 $ and $ y \geq 6 \times 10^5 $

Let Takahashi's initial left and right hand positions be $ (x_{0,0}, y_{0,0}) $ and $ (x_{0,1}, y_{0,1}) $ , respectively, and Aoki's initial left and right hand positions be $ (x_{0,2}, y_{0,2}) $ and $ (x_{0,3}, y_{0,3}) $ , respectively. Let $ K $ be the number of operations. In the $ t $ -th operation ( $ t = 1, 2, \dots, K $ ), Takahashi's left and right hands move to $ (x_{t,0}, y_{t,0}) $ and $ (x_{t,1}, y_{t,1}) $ , respectively, and Aoki's left and right hands move to $ (x_{t,2}, y_{t,2}) $ and $ (x_{t,3}, y_{t,3}) $ , respectively. Then, output to Standard Output in the following format. > $ x_{0,0} $ $ y_{0,0} $ $ x_{0,1} $ $ y_{0,1} $ $ x_{0,2} $ $ y_{0,2} $ $ x_{0,3} $ $ y_{0,3} $ $ \vdots $ $ x_{K,0} $ $ y_{K,0} $ $ x_{K,1} $ $ y_{K,1} $ $ x_{K,2} $ $ y_{K,2} $ $ x_{K,3} $ $ y_{K,3} $ In some inputs, there may be no non-burnable trash, in which case Aoki has no tasks to perform. In such cases, for example, you may output $ x_{t,2} = y_{t,2} = x_{t,3} = y_{t,3} = 0 $ to have Aoki wait in a corner.

### Scoring Let $ X' $ be the number of burnable trash items collected by Takahashi, $ Y' $ be the number of non-burnable trash items collected by Aoki, and $ Z' $ be the number of recyclable trash items that remain uncollected. Let $ T $ be the total time. The score is calculated as follows: - If $ X' + Y' + Z' = X + Y + Z $ and $ T \leq 10^8 $ , then $ \mathrm{round}\left(10^6 \times \left(1 + \log_2 \frac{10^8}{T} \right)\right) $ - If $ X' + Y' + Z' < X + Y + Z $ or $ T > 10^8 $ , then $ \mathrm{round}\left(10^6 \times \frac{X' + Y' + Z'}{X + Y + Z} \right) $ The problem is divided into three subproblems: A, B, and C, based on different input generation methods. Each subproblem contains 150 test cases, and the total score for a submission to that subproblem is the sum of the scores from all test cases in it. If your submission produces an illegal output or exceeds the time limit for some test cases, the submission itself will be judged as WA or TLE , and the score of the submission will be zero. The final ranking is determined by the sum of the highest scores obtained for each subproblem, and there will be no system test after the contest. If more than one team gets the same score, they will be ranked in the same place regardless of the submission time. ### Input Generation - $ \mathrm{rand}(L, U) $ : Generates a random integer uniformly distributed between $ L $ and $ U $ (inclusive). - $ \mathrm{rand\_double}(L, U) $ : Generates a random real number uniformly distributed between $ L $ and $ U $ . - $ \mathrm{normal}(\mu, \sigma) $ : Generates a random real number from a normal distribution with mean $ \mu $ and standard deviation $ \sigma $ . The ranges of the number of non-burnable trash items $ Y $ and recyclable trash items $ Z $ for each problem are as follows: Problem $ Y $ $ Z $ A $ 0 $ from $ 10 $ to $ 100 $ B $ 100 $ $ 0 $ C $ 100 $ from $ 1 $ to $ 100 $ Trash items are generated for each type—in the order of burnable trash → non-burnable trash → recyclable trash—according to the following procedure: 1. Determine the number of trash items $ N $ uniformly at random from the specified range. 2. Determine the number of clusters $ n $ using $ \mathrm{rand}(5,10) $ . 3. For each cluster $ i = 1, \dots, n $ , generate the following parameters: - Weight: $ w_i = \mathrm{rand\_double}(0, 1) $ - Center coordinates: $ cx_i, cy_i = \mathrm{rand}(200000, 800000) $ - Standard deviations: $ \sigma_{x,i}, \sigma_{y,i} = \mathrm{rand}(30000, 90000) $ - Rotation angle: $ \theta_i = \mathrm{rand\_double}(0, \pi) $ 4. Repeat the following process $ N $ times to generate $ N $ trash positions $ (x, y) $ : - Choose a cluster $ i $ at random, with probability proportional to its weight $ w_i $ . - Generate $ x' = \mathrm{normal}(\sigma_{x,i}) $ 、 $ y' = \mathrm{normal}(\sigma_{y,i}) $ . - Compute the coordinates $ (x, y) $ as follows: \\\[ x=\\mathrm{round}(cx\_i+\\cos(\\theta\_i)\\cdot x'-\\sin(\\theta\_i)\\cdot y')\\\\ y=\\mathrm{round}(cy\_i+\\sin(\\theta\_i)\\cdot x'+\\cos(\\theta\_i)\\cdot y') \\\] - Accept the coordinate $ (x, y) $ if it satisfies $ 1 \leq x, y \leq 10^6 - 1 $ and is at least $ 10^3 $ away (Euclidean distance) from any previously generated trash item. Otherwise, retry the generation of $ (x, y) $ . If the type of trash being generated is burnable trash, ensure that there is at least one item in each of the following four regions: - $ x \leq 4 \times 10^5 $ and $ y \leq 4 \times 10^5 $ - $ x \leq 4 \times 10^5 $ and $ y \geq 6 \times 10^5 $ - $ x \geq 6 \times 10^5 $ and $ y \leq 4 \times 10^5 $ - $ x \geq 6 \times 10^5 $ and $ y \geq 6 \times 10^5 $ If this condition is not met, restart the process from the cluster generation step. ### Regarding Problem C **For Problem C, each team may create their own inputs and overwrite the default ones by submitting them.** Refer to the page for Problem D for instructions on how to submit your inputs. Each team may submit four inputs. Among the four submitted inputs, one is randomly selected and made public to all teams, while the remaining three are used for judging. **The input publication and the start of judging are scheduled to take place approximately 3 hours and 30 minutes after the contest begins.** An announcement will be made to all participants once the system is ready. For any team that does not submit their own inputs, four inputs will be generated randomly according to the input generation procedure described earlier. Since each team knows the contents of the inputs they submitted, it is allowed to precompute the corresponding outputs and embed them into the solution program. Submissions to Problem D may be made as many times as desired. However, for each team, only the last submission made **within 180 minutes** from the start of the contest that receives AC will be used for judging. ### Tools (Input generator and score calculation) - [Local version](https://img.atcoder.jp/masters2025-final/ACwJzml3.zip): You need a compilation environment of [Rust language](https://www.rust-lang.org/). - [Pre-compiled binary for Windows](https://img.atcoder.jp/masters2025-final/ACwJzml3_windows.zip): If you are not familiar with the Rust language environment, please use this instead. Please be aware that sharing visualization results or discussing solutions/ideas outside of the team during the contest is prohibited.