AT_mujin_pc_2017_a Robot Racing

你正在开发一种青蛙型机器人。你决定让这些机器人进行一场竞赛。 首先，你将 $N$ 台机器人放置在数轴上。机器人编号为 $1$ 到 $N$。现在，第 $i$ 个机器人位于坐标 $x_i$。其中，所有 $x_i$ 都是整数，并且满足 $0 < x_1 < x_2 < ... < x_N$。 你会不断重复以下操作： - 从数轴上的机器人中选择一台。设选中的机器人的坐标为 $x$。从 $x-1$、$x-2$ 中没有其他机器人占据的位置选择一个作为着陆点。然后让选中的机器人跳到这个着陆点。 当某个机器人的坐标小于等于 $0$ 时，认为它已经到达终点，并立即将其从数轴上移除。你需要不断进行操作，直到所有机器人都到达终点为止。 根据你的操作顺序，$N$ 台机器人到达终点的顺序可能有多种。请问 $N$ 台机器人最终到达终点的顺序有多少种不同的可能？请输出该数对 $10^9+7$ 取模的结果。

输入以如下格式由标准输入给出。 > $N$ $x_1$ $x_2$ ... $x_N$

输出 $N$ 台机器人到达终点的可能顺序数，对 $10^9+7$ 取模的结果。

### 约束 - $2 \leq N \leq 10^5$ - $x_i$ 是整数 - $0 < x_1 < x_2 < ... < x_N \leq 10^9$ ### 部分分数 - 有 $500$ 分的测试点满足 $N \leq 8$ ### 样例解释 1 $3$ 台机器人到达终点的顺序，共有如下 $4$ 种可能： - $(机器人\ 1 \to 机器人\ 2 \to 机器人\ 3)$ - $(机器人\ 1 \to 机器人\ 3 \to 机器人\ 2)$ - $(机器人\ 2 \to 机器人\ 1 \to 机器人\ 3)$ - $(机器人\ 2 \to 机器人\ 3 \to 机器人\ 1)$ ### 样例解释 2 $3$ 台机器人到达终点的顺序，共有如下 $6$ 种可能： - $(机器人\ 1 \to 机器人\ 2 \to 机器人\ 3)$ - $(机器人\ 1 \to 机器人\ 3 \to 机器人\ 2)$ - $(机器人\ 2 \to 机器人\ 1 \to 机器人\ 3)$ - $(机器人\ 2 \to 机器人\ 3 \to 机器人\ 1)$ - $(机器人\ 3 \to 机器人\ 1 \to 机器人\ 2)$ - $(机器人\ 3 \to 机器人\ 2 \to 机器人\ 1)$ 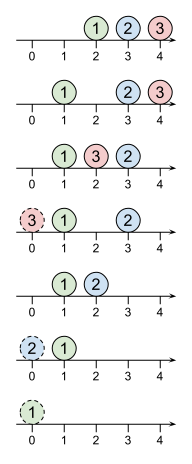例如，按照下图的操作顺序，可以得到 $(机器人\ 3 \to 机器人\ 2 \to 机器人\ 1)$ 的达终顺序。  ### 样例解释 4 请输出答案对 $10^9+7$ 取余的结果。此用例不在部分分数的测试数据范围内。 由 ChatGPT 5 翻译