AT_mujin_pc_2017_b Row to Column

有一个纵向 $N$ 行、横向 $N$ 列的正方形网格。我们用 $(i,j)$ 表示从上往下第 $i$ 行、从左往右第 $j$ 列的格子。 一开始，每个格子都是白色或黑色。网格的初始颜色由一个排成正方形的字符数组 $a_{ij}$（$1 \leq i,j \leq N$）给出。若格子 $(i,j)$ 是白色，则 $a_{ij}$ 为 `.`，若为黑色，则 $a_{ij}$ 为 `#`。 你开发了一个可以重新涂色的机器人。该机器人可以重复进行如下操作： - 可以任意选择整数 $i$ 、$j$ （$1 \leq i, j \leq N$）。将第 $i$ 行的每个格子的颜色分别记为 $c_1, c_2, \ldots, c_N$。接着，用这 $c_1, ..., c_N$ 的颜色，依次将第 $j$ 列的所有格子 $(1,j),(2,j),\ldots,(N,j)$ 的颜色覆盖并更改。 你的目标是让所有格子都变成黑色。请判断能否实现，并在可能的情况下，求出所需操作次数的最小值。

输入以以下形式从标准输入给出： > $N$ > $a_{11}a_{12}\ldots a_{1N}$ > $a_{21}a_{22}\ldots a_{2N}$ > $\vdots$ > $a_{N1}a_{N2}\ldots a_{NN}$

若能将所有格子都变成黑色，则输出所需最小操作次数。若无法实现，则输出 $-1$。

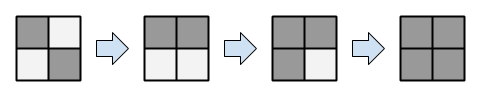
## 限制 - $2 \leq N \leq 500$ - $a_{ij}$ 仅取 `.` 或 `#` ## 部分得分 - 有 $300$ 分的测试数据满足 $N \leq 3$。 ## 样例说明 1 例如，可以按如下方式进行操作，网格颜色会变成如下图所示： - 选择 $i=1$，$j=2$ 进行操作。 - 选择 $i=1$，$j=1$ 进行操作。 - 选择 $i=1$，$j=2$ 进行操作。  由 ChatGPT 5 翻译