AT_mujin_pc_2017_d Oriented Tree

有一棵树 $T$，它包含 $N$ 个顶点，编号为 $1$ 到 $N$。对于每一个 $1 ≤ i ≤ N - 1$，第 $i$ 条边连接顶点 $a_i$ 和 $b_i$。 Snuke 正在通过任意为 $T$ 中的每条边分配方向来构建一个有向图 $T'$。（总共有 $2^{N - 1}$ 种不同的方法来构建 $T'$。） 对于一个固定的 $T'$，我们定义 $d(s,t)$ 对于每个 $1 ≤ s,t ≤ N$，如下： - $d(s,t) = $ 当从顶点 $s$ 到顶点 $t$ 的过程中，必须逆着指定方向遍历的边的数量。 特别地，对于每个 $1 ≤ s ≤ N$，$d(s,s) = 0$。另外，通常情况下，$d(s,t) ≠ d(t,s)$。 我们进一步定义 $D=\max\limits_{1\leq s,t\leq N}d(s,t)$。 Snuke 正在构建 $T'$ 使得 $D$ 的值尽可能小。那么有多少种不同的方法可以构建 $T'$ 以使得 $D$ 的值尽可能小，并且结果对 $10^9 + 7$ 取模？ ### 约束条件 - $2 ≤ N ≤ 1000$ - $1 ≤ a_i,\ b_i ≤ N$ - 给定的图是一个树。

从标准输入接收以下格式的输入： > $N$ $a_1$ $b_1$ $a_2$ $b_2$ $:$ $a_{N - 1}$ $b_{N - 1}$

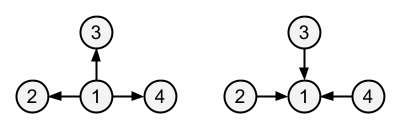
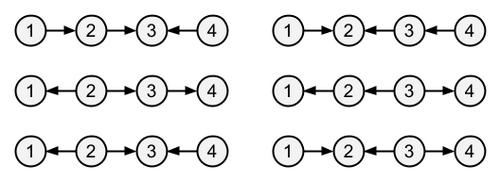
输出使得 $D$ 取最小值的不同构建方式数量，对 $10^9 + 7$ 取模。 ### 样例 $\bm1$ 解释 $D$ 的最小值为 $1$。有两种方式构建 $T'$ 以达到这个值，如下图所示：  ### 样例 $\bm2$ 解释 $D$ 的最小值为 $2$。有六种方式构建 $T'$ 以达到这个值，如下图所示： 

### 制約 - $ 2\