AT_njpc2017_c ハードル走

在数轴上放置了 $N$ 个栏杆。第 $i$ 个栏杆的位置为 $x_i$，其中 $x_i$ 是正整数，并且满足 $x_1 < x_2 < \dots < x_N$。 你是一名跨栏选手。你从数轴原点出发，以恒定速度向正方向奔跑，途中不能改变前进方向。你可以在任意位置（不必是整数坐标）起跳。每次起跳后，你会在空中移动 $L$ 米，然后着陆。但跳跃会消耗体力，因此每次着陆后，在接下来的 $L$ 米内你不能再次起跳，必须在地面上奔跑。最开始你在地面上。 你能否在不碰到任何栏杆的情况下，跨越所有栏杆？ 注意，跨越位置 $x$ 的栏杆，指的是你在 $x$ 处处于空中。此外，起跳和着陆时你都在地面上，因此不能在有栏杆的位置起跳或着陆。你可以在原点起跳。

输入通过标准输入给出，格式如下： > $N$ $L$ $x_1$ $x_2$ $\dots$ $x_N$

如果可以在不碰到任何栏杆的情况下跨越所有栏杆，输出 "YES"（不带引号）；否则输出 "NO"。

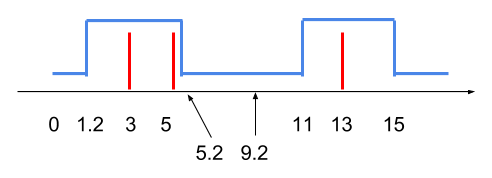
### 限制 - 所有输入均为整数。 - $1 \leq N \leq 10^5$ - $1 \leq L \leq 10^9$ - $1 \leq x_1 < x_2 < \dots < x_N \leq 10^9$ ### 部分分 对于 $400$ 分的测试点，满足以下所有条件： - $1 \leq N \leq 2000$ - $1 \leq L \leq 2000$ - $1 \leq x_1 < x_2 < \dots < x_N \leq 2000$ ### 样例解释 1  图1：输入样例1的跳跃方式示意。图中红线表示栏杆，蓝线表示一种可以跨越所有栏杆的前进方式。在这种方式下，首先在 $0 \leq x \leq 1.2$ 区间地面奔跑，然后在 $x = 1.2$ 处起跳，于 $1.2 < x < 5.2$ 区间空中前进。由于跳跃影响，$5.2 \leq x \leq 9.2$ 区间必须在地面奔跑。之后在 $x = 11$ 处起跳，就可以跨越所有栏杆。本例满足部分分限制。 ### 样例解释 2 无论如何起跳，都无法跨越 $x = 5$ 处的栏杆。本例满足部分分限制。 ### 样例解释 3 例如在原点起跳，可以跨越所有栏杆。本例满足部分分限制。 ### 样例解释 4 不能从原点向负方向移动。本例满足部分分限制。 ### 样例解释 5 本例满足部分分限制。 ### 样例解释 6 本例满足部分分限制。 由 ChatGPT 4.1 翻译