AT_oupc2023_day1_m Can't Be UT

在 $xy$ 平面上有 $N$ 片银杏叶。每一片银杏叶的形状均为圆形，第 $i$ 片银杏叶的圆心坐标为 $(A_i,B_i)$，且所有银杏叶的半径都相等。 现在我们要为这 $N$ 片银杏叶涂色。在涂色前，KowerKoint 君心情平静，但如果涂色结束后，存在满足以下条件的某对 $(i, j)$（$1 \leq i < j \leq N$），他就会变得焦躁不安： - 第 $i$ 片银杏叶的内部（不含圆周）与第 $j$ 片银杏叶的内部（不含圆周）有公共部分； - 第 $i$ 片银杏叶和第 $j$ 片银杏叶的颜色不同。 KowerKoint 君喜欢多彩的风景，因此希望至少有 $C$ 种不同的颜色被涂在 $1$ 片或更多银杏叶上。在满足上述条件，使得KowerKoint君始终平静的前提下，求银杏叶半径的最大值。已知在题目约束下，最大值总是存在且有解。

输入按如下格式从标准输入读入。 > $N$ $C$ $A_1$ $B_1$ $A_2$ $B_2$ $\vdots$ $A_N$ $B_N$

请输出答案一行。 当你的答案与标准答案的绝对误差或相对误差不超过 $10^{-6}$ 时，即视为正确。

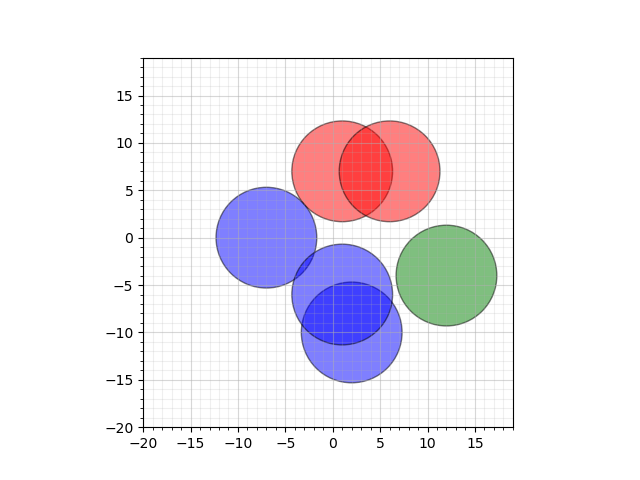
## 小课题 1. ($1$ 分) $N \leq 1{,}000$ 2. ($99$ 分) 无额外约束 ## 样例解释 1 当半径不超过 $\frac{\sqrt{113}}{2}=5.31507291\dots$ 时，可以如下图为 $3$ 种不同颜色。 本测试用例满足小课题 1 的限制。  ## 样例解释 2 本测试用例满足小课题 1 的限制。 # 数据范围 - $2 \leq C \leq N \leq 50{,}000$ - $-10{,}000 \leq A_i, B_i \leq 10{,}000$ - 所有 $(A_i, B_i)$ 均互不相同 - 输入均为整数 由 ChatGPT 5 翻译