AT_oupc2023_day1_m Can't Be UT

$ xy $ 平面上にイチョウの葉が $ N $ 枚あります。 $ N $ 枚のイチョウの葉はすべて円の形をしており、 $ i $ 番目のイチョウの葉の中心の座標は $ (A_i,B_i) $ で、半径はすべて等しいです。 今からこれら $ N $ 枚のイチョウの葉に色を付けます。 色を付ける前 KowerKoint 君は落ち着いていますが、色を付け終わったあと以下の条件を満たすような $ (i,j) $ ( $ 1\leq i < j \leq N $ ) が存在すると落ち着きをなくします。 - $ i $ 番目のイチョウの葉の内部（周は含まれない）と $ j $ 番目のイチョウの葉の内部（周は含まれない）の共通部分が空ではない - $ i $ 番目のイチョウの葉の色と $ j $ 番目のイチョウの葉の色が異なる KowerKoint 君はカラフルな風景が好きなので、 $ 1 $ 枚以上のイチョウの葉につけられた色の種類数が $ C $ 以上になるようにしたいです。 このような色の付け方で、色を付け終わったあとも KowerKoint 君が落ち着いていられるようなものが存在するようなイチョウの葉の半径の最大値を求めてください。 制約内で、最大値が常に存在することが証明できます。

入力は以下の形式で標準入力から与えられます。 > $ N $ $ C $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ $ \vdots $ $ A_N $ $ B_N $

答えを $ 1 $ 行で出力してください。 正しい値との絶対誤差または相対誤差が $ 10^{-6} $ 以下であるとき、正しいとみなされます。

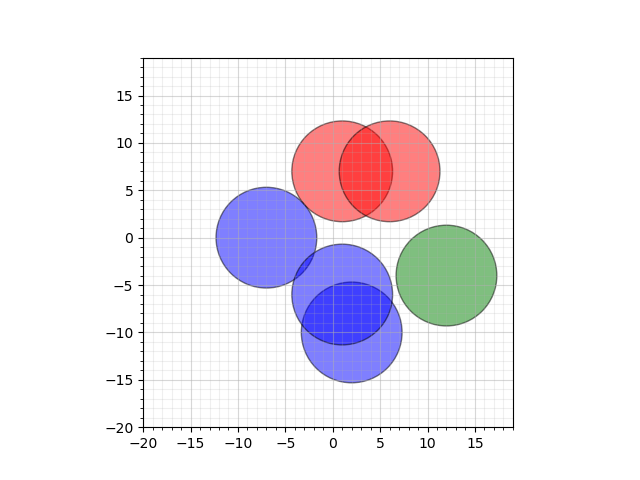
### 小課題 1. ( $ 1 $ 点) $ N \leq 1{,}000 $ 2. ( $ 99 $ 点) 追加の制約はない ### Sample Explanation 1 半径が $ \frac{\sqrt{113}}{2}=5.31507291\dots $ 以下のとき、下の図のように $ 3 $ 種類の色をつけることができます。 このテストケースは小課題 1 の制約を満たします。  ### Sample Explanation 2 このテストケースは小課題 1 の制約を満たします。 ### Constraints - $ 2 \leq C \leq N \leq 50{,}000 $ - $ -10{,}000 \leq A_i, B_i \leq 10{,}000 $ - $ (A_i,B_i) $ はすべて異なる - 入力はすべて整数