AT_pakencamp_2018_day2_e クリスマスツリー　(Tree Coloring)

[problemUrl]: https://atcoder.jp/contests/pakencamp-2018-day2/tasks/pakencamp_2018_day2_e 今日はクリスマス・イブである。PAKEN 君は、平成最後のクリスマスに向けて、以下のようなデコレーションを作りました。 - デコレーションは、「電球」と「棒」で構成される。デコレーションは、以下のようにして作られる。 - 電球 $ (a,\ b) $ $ (0\ \leq\ a\ \leq\ D,\ -a\ \leq\ b\ \leq\ a) $ を満たす整数の組) を作る。$ a $ を「深さ」と呼び、$ b $ を「横座標」と呼ぶ。 - 電球 $ (0,\ 0) $ と $ (1,\ -1) $ を、そして電球 $ (0,\ 0) $ と $ (1,\ 1) $ を、直接棒で結ぶ。 - 同じ深さで横座標が $ 1 $ しか違わない電球同士を、直接棒で結ぶ。 - 電球 $ (a,\ -(a-1)) $ と $ (a+1,\ -(a+1)) $ を、そして電球 $ (a,\ a-1) $ と $ (a+1,\ a+1) $ を、直接棒で結ぶ。 例えば、$ D\ =\ 1,\ 2,\ 3 $ のとき、グラフは以下の図のようになります。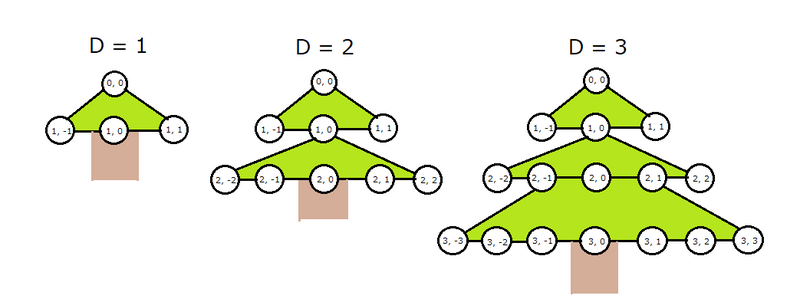  どうやらクリスマスツリーみたいな感じです。 PAKEN 君は、色 $ 1 $ から $ X $ までの $ X $ 個の色を使って、全ての電球に色を付けたいです。ただし、棒で直接結ばれた電球は同じ色であってはいけません。 色の付け方は何通りあるか、$ 1\ 000\ 000\ 007 $ で割った余りを求めてください。

入力は以下の形式で標準入力から与えられます。 > $ D $ $ X $

色の付け方は何通りあるか、$ 1\ 000\ 000\ 007 $ で割った余りを一行に出力してください。

### 制約 - $ D $ は $ 1 $ 以上 $ 10\ 000\ 000 $ 以下の整数 - $ X $ は $ 1 $ 以上 $ 1\ 000\ 000\ 000 $ 以下の整数 ### 小課題 小課題 $ 1 $ \[$ 2 $ 点\] 入力は以下の条件を満たす。 - $ D\ =\ 1 $ - $ X\ \leq\ 4 $ 小課題 $ 2 $ \[$ 12 $ 点\] 入力は以下の条件を満たす。 - $ D\ \leq\ 2 $ - $ X\ \leq\ 6 $ 小課題 $ 3 $ \[$ 21 $ 点\] 入力は以下の条件を満たす。 - $ D\ \leq\ 4 $ - $ X\ \leq\ 7 $ 小課題 $ 4 $ \[$ 31 $ 点\] 入力は以下の条件を満たす。 - $ D\ \leq\ 50 $ - $ X\ \leq\ 25 $ 小課題 $ 5 $ \[$ 18 $ 点\] - $ D\ \leq\ 50 $ を満たす。 小課題 $ 6 $ \[$ 11 $ 点\] - $ D\ \leq\ 100\ 000 $ を満たす。 小課題 $ 7 $ \[$ 5 $ 点\] - 追加の制約はない。 ### Sample Explanation 1 以下の $ 2 $ 通りの塗り方が存在します。 !\[ \](https://img.atcoder.jp/pakencamp-2018-day2/83bf7fd0dc8341157661089dece0219b.png) ### Sample Explanation 2 以下の $ 18 $ 通りの塗り方が存在します。 !\[ \](https://img.atcoder.jp/pakencamp-2018-day2/9cb66e828bc68ac034393530654430fe.png) この入力は、小課題 $ 1 $ の制約を満たします。 ### Sample Explanation 3 この入力は、小課題 $ 2 $ の制約は満たしませんが、小課題 $ 3 $ の制約を満たします。