AT_pakencamp_2018_day2_f 同一経路　(Samepath)

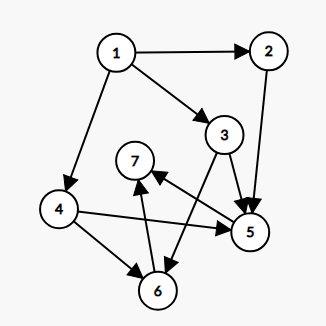
PAKEN 市长 E869120 计划在市内建设若干个检查点，以及连接两个检查点的若干条单向道路。 设检查点的数量为 $N$，并将检查点编号为 $1, 2, 3, \ldots, N$。 自古以来，这个城市的幸运数字是 $K$。 因此，市长决定按照以下条件进行建设： - 从检查点 $1$ 到 $N$ 的路径总数恰好为 $K$。 - 从检查点 $1$ 到 $N$ 的所有路径中，无论选择哪一条，经过的道路数都相同。 例如，当 $K = 5$ 时，下图所示的检查点和道路的配置满足条件。因为从检查点 $1$ 到 $N$ 的路径总数为 $K = 5$，且所有路径都恰好经过 $3$ 条道路。  由于成本原因，市长希望检查点的数量 $N$ 尽可能小。 请给出一种满足上述条件的建设方案。**但要求：只能建设 $a < b$ 的道路（即只能从编号小的检查点通向编号大的检查点），且不能有多条连接同一对检查点的道路。**

输入通过标准输入按以下格式给出。 > $K$

输出按以下格式给出。 > $N$ $M$ > $a_1$ $b_1$ > $a_2$ $b_2$ > $a_3$ $b_3$ > $\cdots$ > $a_M$ $b_M$ - 第 $1$ 行输出检查点数量 $N$ 和道路数量 $M$，以空格分隔。 - 接下来 $M$ 行，每行输出一条道路的信息。$a_i, b_i$ 表示第 $i$ 条道路直接连接检查点 $a_i$ 到 $b_i$。**要求 $a_i < b_i$。** - 最后需换行。**要求 $N \leq 200$，否则判为 Wrong Answer。** **并且，$(a_i, b_i) \neq (a_j, b_j)\ (i \neq j)$ 且 $a_i < b_i$。**

### 数据范围 - $K$ 是 $1$ 到 $10^{18}$ 之间的整数。 ### 子任务 子任务 $1$ [$8$ 分] - $K \leq 150$。 子任务 $2$ [$12$ 分] - $K \leq 8\,000$。 子任务 $3$ [$80$ 分] - 无额外限制。 对于子任务 $3$，评测方式如下。设 $L$ 为所有测试用例中 $N$ 的最大值。 - $161 \leq L \leq 200$ 时，$15$ 分 - $152 \leq L \leq 160$ 时，$55 - (L - 150) \times 2$ 分 - $L = 151$ 时，$65$ 分 - $L \leq 150$ 时，$80$ 分 ### 样例解释 1 如下图所示，从检查点 $1$ 到 $7$ 有 $5$ 条路径，且所有路径都经过相同数量（$3$ 条）的道路，满足条件。  ### 样例解释 2 如下图所示，从检查点 $1$ 到 $16$ 有 $20$ 条路径，且所有路径都经过相同数量（$6$ 条）的道路，满足条件。  ### 样例解释 3 该输入满足子任务 $1$ 的限制。 由 ChatGPT 4.1 翻译