AT_pakencamp_2018_day2_f 同一経路　(Samepath)

[problemUrl]: https://atcoder.jp/contests/pakencamp-2018-day2/tasks/pakencamp_2018_day2_f PAKEN 市長の E869120 氏は、市にいくつかのチェックポイントと、$ 2 $ つのチェックポイントを結ぶいくつかの一方通行の道路を建設することを計画しました。 チェックポイントの数を $ N $ とし、チェックポイントを $ 1,\ 2,\ 3,\ ...,\ N $ と番号付けするものとします。 太古の時代から、この市のラッキーナンバーは $ K $ とされています。 そのため、市長は以下のような条件を満たすものを建設することに決めました。 - チェックポイント $ 1 $ から $ N $ まで行く方法の通り数が、ちょうど $ K $ 通りである。 - チェックポイント $ 1 $ から $ N $ まで行く方法のうち、どの経路を選んで通っても、通る道路の本数は変わらない。 例えば、$ K\ =\ 5 $ のとき、以下のチェックポイントと道路の配置は条件を満たします。何故なら、チェックポイント $ 1 $ から $ N $ まで行く方法の総数は $ K\ =\ 5 $ 通りであり、全ての行き方についてちょうど $ 3 $ 本の道を通るからです。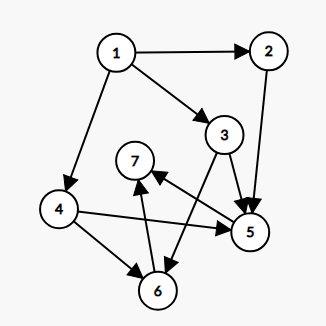  コストの関係上、市長はできるだけチェックポイントの数 $ N $ をできるだけ小さくしたいです。 このような条件を建設の仕方を $ 1 $ つ構成してください。**ただし、チェックポイント $ a $ から $ b $ まで直接行く道路は $ a\

入力は以下の形式で標準入力から与えられる。 > $ K $

出力は以下の形式で行うこと。 > $ N $ $ M $ $ a_1 $ $ b_1 $ $ a_2 $ $ b_2 $ $ a_3 $ $ b_3 $ ... $ a_M $ $ b_M $ - $ 1 $ 行目には、チェックポイントの数 $ N $ と、道路の数 $ M $ を空白区切りで出力してください。 - $ 2 $ 行目から $ M $ 行にわたって、道の情報を出力してください。ただし、$ a_i,\ b_i $ は、「$ i $ 番目の道路がチェックポイント $ a_i $ から $ b_i $ へ直接結ぶ」ことを表します。**このとき $ a_i\

### 制約 - $ K $ は $ 1 $ 以上 $ 10^{18} $ 以下の整数 ### 小課題 小課題 $ 1 $ \[$ 8 $ 点\] - $ K\ \leq\ 150 $ を満たす。 小課題 $ 2 $ \[$ 12 $ 点\] - $ K\ \leq\ 8\ 000 $ を満たす。 小課題 $ 3 $ \[$ 80 $ 点\] - 追加の制約はない。 ただし、小課題 $ 3 $ について、採点は以下のように行われます。そこでは、$ L $ を「全てのテストケースにおける $ N $ の最大値」とします。 - $ 161\ \leq\ L\ \leq\ 200 $ の場合、$ 15 $ 点 - $ 152\ \leq\ L\ \leq\ 160 $ の場合、$ 55\ -\ (L\ -\ 150)\ *\ 2 $ 点 - $ L\ =\ 151 $ の場合、$ 65 $ 点 - $ L\ \leq\ 150 $ の場合、$ 80 $ 点満点 ### Sample Explanation 1 以下の図において、チェックポイント $ 1 $ から $ 7 $ まで行くのに $ 5 $ 通りの方法が存在し、全て同じ本数 ($ 3 $ 本) の道路を通るため、条件を満たします。 !\[ \](https://img.atcoder.jp/pakencamp-2018-day2/457542e86b6cd161655104d58029b46e.png) ### Sample Explanation 2 以下の図において、チェックポイント $ 1 $ から $ 16 $ まで行くのに $ 20 $ 通りの方法が存在し、全て同じ本数 ($ 6 $ 本) の道路を通るため、条件を満たします。 !\[ \](https://img.atcoder.jp/pakencamp-2018-day2/e4a27202d79a6c7e86e60ae6e1d14799.png) ### Sample Explanation 3 この入力は、小課題 $ 1 $ の制約を満たします。