AT_pakencamp_2018_day2_h プレゼント配り　(Santa Claus' Track)

[problemUrl]: https://atcoder.jp/contests/pakencamp-2018-day2/tasks/pakencamp_2018_day2_h サンタクロースは、PAKEN CITY という街でプレゼントを配ります。 PAKEN CITY は $ (2N+1)\ \times\ (2N+1) $ のマス目で表される街で、北から $ i+1 $ マス目、西から $ j+1 $ マス目のマスを $ (i,\ j) $ で表します。 このとき、$ i $ を「行番号」、$ j $ を「列番号」ということにします。 PAKEN CITY の各マスは、「道路」「更地」「家」のいずれかです。 行番号と列番号のどちらかが偶数のマスはすべて道路であり、両方奇数のマスは更地または家です。 入力で与えられる $ S_{R,\ C} $ はマス $ (2R+1,\ 2C+1) $ に対応しており、`.` のとき「更地」であり、`1`〜`9` のとき家であり、この数字は家に住む人数を表します。 サンタクロースの $ reiji1112 $ 君は、ある道路の交差点 (行番号、列番号が両方偶数のマス) からスタートして、同じマスを 2 度通らずに $ K $ 個以下の交差点を通って元の場所に戻る経路をたどってプレゼントを配ります。 また、家に ($ 4 $ 方向に) 隣接するマスから、この家にプレゼントを配ることができます。1 つの家に配れるプレゼントは、この家に住む人数までです。また、同じ家に $ 2 $ 回以上プレゼントを配ることはできません。 サンタクロースができるだけ多くのプレゼントを配れるような、移動経路を作ってください。 サンタの移動経路の例は、以下の入力の場合、次のようになります。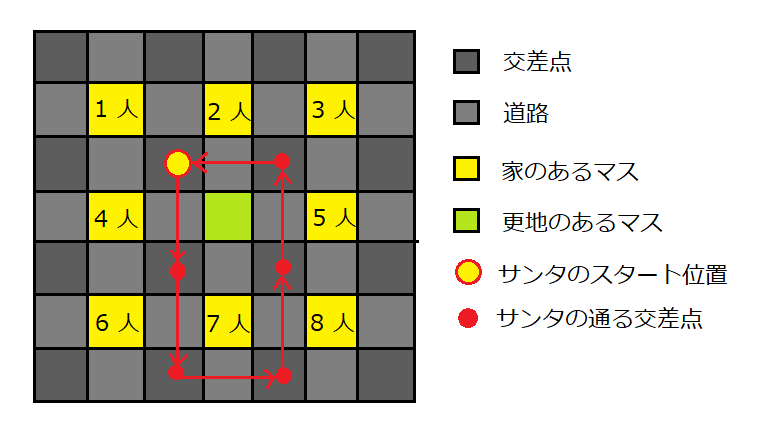 ``` 3 6 123 4.5 678 ```  この場合、$ 2\ +\ 4\ +\ 5\ +\ 6\ +\ 7\ +\ 8\ =\ 32 $ 人に対してプレゼントを配ることができます。

> $ N $ $ K $ $ S_{0,0}S_{0,1}S_{0,2}...S_{0,N-1} $ $ S_{1,0}S_{1,1}S_{1,2}...S_{1,N-1} $ $ S_{2,0}S_{2,1}S_{2,2}...S_{2,N-1} $ : : : $ S_{N-1,0}S_{N-1,1}S_{N-1,2}...S_{N-1,N-1} $

スタートする交差点の座標が $ (2R,\ 2C) $ とし、最初の位置から順に、「東、西、南、北方向に $ 2 $ マス進むとき、それぞれ `R`, `L`, `D`, `U`」をつなげた $ K $ 文字以下の文字列を $ X $ とするとき、各ケースに対して： > $ R $ $ C $ $ X $ と出力してください。$ X $ の文字数はそのケースにおける $ K $ 文字以下にしてください。例えば、問題文中の図の例における出力は `1 1 DDRUUL` となります。しかし、いくつかのケースの結果が得られていないときは、そのケースに対して代わりに： > $ -1 $ $ -1 $ $ -1 $ と出力してください。 全部で $ 6 $ ケースあるので、ケース $ 1 $ から順に $ 6 $ 行で出力してください。 ただし、この問題は Output Only 形式で、入力データも与えられているので、手元の環境で答えを求める場合は Text(cat) 言語 (出力そのままの文字列) で提出することを推奨します。 ``` 1 1 DDRUUL -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 ``` このように、$ 6 $ 行で出力してください。しかし、このような出力をしても $ 0 $ 点となります。詳しくは、「得点」の項をご覧ください。 **なお、スタートした場所に戻ってくる経路ではない場合や、$ X $ が $ K $ 文字を超えた場合、PAKEN CITY からはみ出るような経路を出力した場合、WA などのエラーが出ますのでご注意ください。**

### ケースについて ケースは、次のようになっている。 ケース番号 得点 $ N $ $ K $ $ V_1 $ $ V_2 $ $ V_3 $ $ V_4 $ $ V_5 $ \#1 10 9 24 220 260 271 - - \#2 18 100 280 2766 2937 3051 3110 3230 \#3 18 500 1400 13299 14104 14641 14940 15820 \#4 18 500 1400 3346 3975 4394 4600 5060 \#5 18 500 1400 11368 15543 16198 16600 17490 \#6 18 100 1000 8950 9783 10338 10660 11310入力データは、次の [ZIP ファイル](https://goo.gl/M3m7fH) をダウンロードすることで入手できます。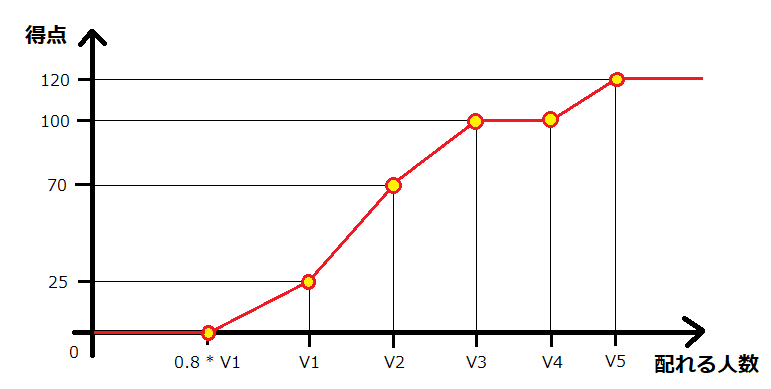 ### 得点 先ほどの「ケース」の部分で、$ V_1,\ V_2,\ V_3,\ V_4,\ V_5 $ という値が決まっていましたが、これは得点に関係します。 - まず、$ V_1 $ は $ 25 $ パーセント点のラインです。この 0.8 倍以下になると $ 0 $ 点であり、$ 0.8 $ 倍〜$ 1 $ 倍のとき、点数は 1 次関数的に増えます。 - 次に、$ V_2 $ は $ 70 $ パーセント点のラインです。$ V_1 $ から $ V_2 $ の間も点数は 1 次関数的に増えます。 - 次に、$ V_3 $ は $ 100 $ パーセント点のラインです。$ V_2 $ から $ V_3 $ の間も点数は 1 次関数的に増えます。 - $ V_3 $ から $ V_4 $ まではすべで $ 100 $ パーセント点です。 - スコア $ V_4 $ を超えると、スコア $ V_5 $ まで点数が 1 次関数的に増え、$ V_5 $ のときに最大の点数 120 パーセント点になります。 すなわち、得点の変化は以下のグラフのようになります。