AT_pakencamp_2019_day2_a パ研君と塗り絵

パ研君正在努力练习涂色画，目标是参加国际涂色奥林匹克。 现在，他准备了一个 $N \times N$ 的方格。我们用 $(i, j)$ 表示从上往下第 $i$ 行、从左往右第 $j$ 列的格子。特别地，左上角的格子是 $(1, 1)$，右下角的格子是 $(N, N)$。 他打算用 $K$ 种颜色（颜色 $1$、颜色 $2$、颜色 $3$、……、颜色 $K$）来给每个格子上色。也可以有些格子不涂色。 此时，完成的涂色画需要满足以下条件： - 对于所有满足 $1 \leq i \leq K$ 的整数 $i$，都要满足以下条件： - 如果存在至少一个格子被颜色 $i$ 涂色，则所有被颜色 $i$ 涂色的格子必须连通。 - 也就是说，任意两个被颜色 $i$ 涂色的不同格子 $(x_1, y_1)$、$(x_2, y_2)$，都可以只经过上下左右相邻且被颜色 $i$ 涂色的格子，从 $(x_1, y_1)$ 走到 $(x_2, y_2)$。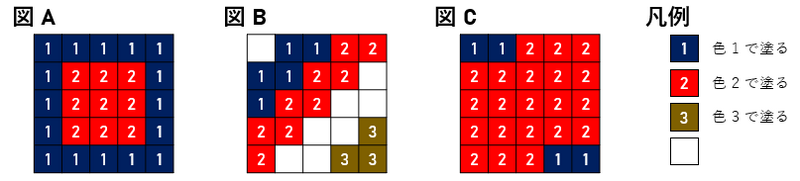 例如，图 (A)、图 (B) 的涂色方式满足条件，但图 (C) 中颜色 $1$ 的格子不连通，因此不满足条件。  此外，完成的涂色画会按如下方式计分： - 用 $V_1$ 表示被某种颜色 $A_{i, j}$ 涂色的格子的总数。 - 对于每个 $i$（$1 \leq i \leq Q$），如果在格子 $(r_i, c_i)$、$(r_i, c_i+1)$、$(r_i, c_i+2)$、……、$(r_i, c_i+K-1)$ 这 $K$ 个格子中，恰好各有一个格子分别被颜色 $1$、颜色 $2$、颜色 $3$、……、颜色 $K$ 涂色，则这样的 $i$ 的个数记为 $V_2$。 - 此时涂色画的得分为 $100 \times V_2 + V_1$。如果不满足上述连通性条件，则得分为 $0$。 请你给出一种涂色方案，使得得分尽可能高。

输入以如下格式从标准输入读入： > $N$ $K$ $Q$ $A_{1,1}$ $A_{1,2}$ ... $A_{1,N}$ $A_{2,1}$ $A_{2,2}$ ... $A_{2,N}$ : $A_{N,1}$ $A_{N,2}$ ... $A_{N,N}$ $r_1$ $c_1$ $r_2$ $c_2$ : $r_Q$ $c_Q$

请按如下格式输出（共 $N$ 行）： > $S_{1,1}$ $S_{1,2}$ $S_{1,3}$ ... $S_{1,N}$ > $S_{2,1}$ $S_{2,2}$ $S_{2,3}$ ... $S_{2,N}$ > $S_{3,1}$ $S_{3,2}$ $S_{3,3}$ ... $S_{3,N}$ > ... > $S_{N,1}$ $S_{N,2}$ $S_{N,3}$ ... $S_{N,N}$ 其中，$S_{i,j}$ 表示格子 $(i, j)$ 用哪种颜色涂色。如果用颜色 $x$ 涂色，则 $S_{i,j} = x$；如果不涂色，则 $S_{i,j} = 0$。 如果输出不符合上述格式，或者 $0 \leq S_{i,j} \leq K$ 不成立，或者不满足题目中的涂色条件，则判为“不正确”。对于输入样例中的测试点，该测试点得分为 $0$；对于其他测试点，则所有非样例测试点得分均为 $0$。

### 数据范围 - $N = 100$ - $Q = 240$ - $K = 4$ - $1 \leq A_{i,j} \leq K$ - $1 \leq r_i \leq N$ - $1 \leq c_i \leq N - K + 1$ - 若 $r_i = r_j$ 且 $i \neq j$，则 $|c_i - c_j| \geq K$。 - 输入均为整数。 ### 测试数据生成方式 - $A_{i, j}$ 的值是从 $1$ 到 $K$ 的整数中等概率随机选取的。 - $(r_i, c_i)$ 的生成方式如下： 1. 对 $i = 1, 2, 3, ..., Q$ 依次执行步骤 2～4。 2. 首先，从 $1$ 到 $N$ 的整数中等概率随机选取 $r_i$。 3. 然后，从 $1$ 到 $N-K+1$ 的整数中等概率随机选取 $c_i$。 4. 如果存在 $1 \leq j < i$ 使得 $r_i = r_j$ 且 $|c_i - c_j| \leq K-1$，则回到步骤 2 重新选取 $r_i, c_i$。否则，继续下一个 $i$。 ### 输入输出样例 输入样例及输出样例可从[此链接](https://img.atcoder.jp/pakencamp-2019-day2/b6ea69e60b1bce4a99491680c453d05d.zip)下载。 这些样例也包含在实际测试点中，并计入总得分，请注意。 由 ChatGPT 4.1 翻译