AT_pakencamp_2019_day2_a パ研君と塗り絵

[problemUrl]: https://atcoder.jp/contests/pakencamp-2019-day2/tasks/pakencamp_2019_day2_a パ研君は国際塗り絵オリンピックを目指し，日々塗り絵に取り組んでいます． さて，彼は塗り絵を作るために $ N\ \times\ N $ のマス目を用意しました．このマス目の上から $ i $ 行目で左から $ j $ 行目のマスを $ (i,\ j) $ とします．特に，左上のマスは $ (1,\ 1) $，右下のマスは $ (N,\ N) $ です． 彼は，それぞれのマスを，色 $ 1 $，色 $ 2 $，色 $ 3 $，...，色 $ K $ の $ K $ 色を用いて，色を塗ることにしました．ただし，色を塗らないマスがあってもよいです． このとき，完成した塗り絵は，次の条件を満たさなければなりません． - $ 1\ \leq\ i\ \leq\ K $ を満たす，すべての整数 $ i $ について，以下の条件を満たす． - 色 $ i $ で塗られたマスが $ 1 $ 個以上存在する場合，色 $ i $ で塗られたマス全体は連結である． - つまり，色 $ i $ で塗られた相異なる $ 2 $ つのマス $ (x_1,\ y_1),\ (x_2,\ y_2) $ を考えたとき，どのような $ ((x_1,\ y_1),\ (x_2,\ y_2)) $ の組であっても，マス $ (x_1,\ y_1) $ からマス $ (x_2,\ y_2) $ まで，上下左右に隣り合う色 $ i $ のマスのみをたどって行くことができる． 例えば，図 (A)，図 (B) のような塗り絵は条件を満たしますが，図 (C) は色 $ 1 $ で塗られたマス全体が連結ではないため，条件を満たしません．  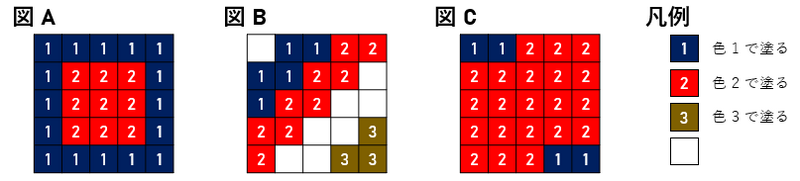また，完成した塗り絵は，以下のように点数で評価されます． - マス $ (i,\ j) $ が色 $ A_{i,\ j} $ で塗られているような，マスの個数を $ V_1 $ とする． - マス $ (r_i,\ c_i) $，$ (r_i,\ c_i+1) $，$ (r_i,\ c_i+2) $，...，$ (r_i,\ c_i+K-1) $ のうち，色 $ 1 $，色 $ 2 $，色 $ 3 $，...，色 $ K $ で塗られているマスが $ 1 $ 個ずつ存在するような，$ i $ の個数 $ (1\ \leq\ i\ \leq\ Q) $ を $ V_2 $ とする． - そのときの塗り絵の点数は，$ 100\ \times\ V_2\ +\ V_1 $ 点である．なお，条件を満たさない塗り絵は $ 0 $ 点となる． このとき，できるだけ高い点数を得られるように，マス目を塗ってください．

入力は, 以下の形式で標準入力から与えられます． > $ N $ $ K $ $ Q $ $ A_{1,1} $ $ A_{1,2} $ ... $ A_{1,N} $ $ A_{2,1} $ $ A_{2,2} $ ... $ A_{2,N} $ : $ A_{N,1} $ $ A_{N,2} $ ... $ A_{N,N} $ $ r_1 $ $ c_1 $ $ r_2 $ $ c_2 $ : $ r_Q $ $ c_Q $

以下の形式で出力してください．($ N $ 行に渡って出力すること．) > $ S_{1,\ 1} $ $ S_{1,\ 2} $ $ S_{1,\ 3} $ ... $ S_{1,\ N} $ $ S_{2,\ 1} $ $ S_{2,\ 2} $ $ S_{2,\ 3} $ ... $ S_{2,\ N} $ $ S_{3,\ 1} $ $ S_{3,\ 2} $ $ S_{3,\ 3} $ ... $ S_{3,\ N} $ : $ S_{N,\ 1} $ $ S_{N,\ 2} $ $ S_{N,\ 3} $ ... $ S_{N,\ N} $ ただし、$ S_{i,\ j} $ は，マス $ (i,\ j) $ をどの色で塗るかを表します．マス $ (i,\ j) $ を色 $ x $ で塗る場合，$ S_{i,\ j}\ =\ x $ であり，塗らない場合は $ S_{i,\ j}\ =\ 0 $ です． また，上記のフォーマットに違反する出力や，$ 0\ \leq\ S_{i,\ j}\ \leq\ K $ を満たさない出力，問題文中の塗り方の条件を満たさない出力は「不正解」と判定されます．この場合，そのテストケースが入力例として与えられているものであれば，そのテストケースでの得点が $ 0 $ 点となります．その他のテストケースであれば，入力例以外のすべてのテストケースでの $ 0 $ 点となります．

### 制約 - $ N\ =\ 100 $ - $ Q\ =\ 240 $ - $ K\ =\ 4 $ - $ 1\ \leq\ A_{i,j}\ \leq\ K $ - $ 1\ \leq\ r_i\ \leq\ N $ - $ 1\ \leq\ c_i\ \leq\ N\ -\ K\ +\ 1 $ - $ r_i\ =\ r_j\ (i\ \neq\ j) $ のとき，$ |c_i\ -\ c_j|\ \geq\ K $ を満たす． - 入力はすべて整数である． ### テストケース生成方法 - $ A_{i,\ j} $ の値は，$ 1 $ 以上 $ K $ 以下の整数から一様ランダムに選ばれる． - $ (r_i,\ c_i) $ の値は，以下のように決まる． 1. $ i\ =\ 1,\ 2,\ 3,\ ...,\ Q $ の順番に，操作 2. ～ 4. を行う． 2. まず，$ r_i $ を $ 1 $ 以上 $ N $ 以下の整数から一様ランダムに選ぶ． 3. 次に，$ c_i $ を $ 1 $ 以上 $ N-K+1 $ 以下の整数から一様ランダムに選ぶ． 4. $ r_i=r_j $ かつ $ |c_i\ -\ c_j|\ \leq\ K-1 $ を満たす $ 1 $ 以上 $ i-1 $ 以下の整数 $ j $ が存在すれば，2. に戻り $ (r_i,\ c_i) $ を決めなおす．そうでない場合 1. に戻り，次の $ i $ の値に対して操作を行う． ### 入出力例 入力例および出力例は，[このリンク](https://img.atcoder.jp/pakencamp-2019-day2/b6ea69e60b1bce4a99491680c453d05d.zip)からダウンロードできます． なお，これらの例も実際のテストケースに含まれ，得点の一部に加算されることにご注意ください．