AT_pakencamp_2019_day3_d パ研軍旗

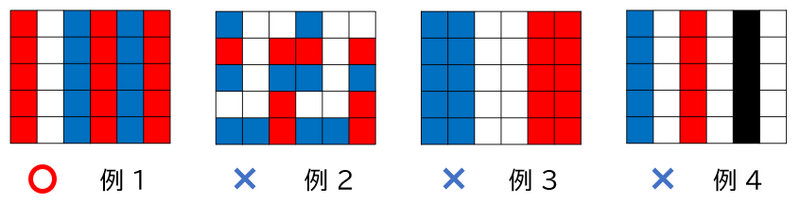
筑駒パ研即将迎来一场“パ研战争”。为此，他们决定制作一面军旗。 旗帜的设计由纵向 $5$ 行、横向 $N$ 列组成的 $5\times N$ 的格子表示。我们用 $(i, j)$ 表示从上到下第 $i$ 行、从左到右第 $j$ 列的格子。 目前，旗帜上的每个格子都被涂成了红、蓝、白、黑中的一种颜色。更具体地说，格子 $(i, j)$ 被颜色 $S_{i, j}$ 涂色，其中 $S_{i, j}$ 是 `R`、`B`、`W`、`#` 之一，分别表示红、蓝、白、黑。 E869120 君希望将パ研军旗重新涂色，使其满足以下条件： - 对于所有 $N$ 列，每一列的 $5$ 个格子要么全是蓝色、要么全是白色、要么全是红色。 - 任意相邻的两列颜色必须不同。 注意，如果存在黑色格子，则无法满足条件。 以下是满足条件和不满足条件的旗帜示例。  - 示例 $1$ 满足条件。 - 示例 $2$，例如从左起第 $2$ 列存在蓝色和白色格子，未满足“5 个格子必须全为同色”的条件。 - 示例 $3$，例如从左起第 $3$ 列和第 $4$ 列颜色相同，未满足条件。 - 示例 $4$，例如从左起第 $5$ 列存在黑色格子，未满足条件。 E869120 君希望尽可能减少需要重新涂色的格子数，以缩短旗帜制作时间。 请编写程序，求出最少需要重新涂色的格子数。

输入通过标准输入给出。 注意，每一行的颜色信息 $S_{i, 1}, S_{i, 2}, S_{i, 3}, \dots, S_{i, N}$ 作为长度为 $N$ 的字符串输入。 > $N$ > $S_{1, 1}S_{1, 2}S_{1, 3}\cdots S_{1, N}$ > $S_{2, 1}S_{2, 2}S_{2, 3}\cdots S_{2, N}$ > $S_{3, 1}S_{3, 2}S_{3, 3}\cdots S_{3, N}$ > $S_{4, 1}S_{4, 2}S_{4, 3}\cdots S_{4, N}$ > $S_{5, 1}S_{5, 2}S_{5, 3}\cdots S_{5, N}$

请输出制作パ研军旗时需要重新涂色的最少格子数。

### 约束条件 所有输入数据满足以下约束： - $1 \leq N \leq 999$ - $S_{i, j}$ 为 `R`、`B`、`W`、`#` 之一 ### 部分得分 本题分为若干小题，若某个小题的所有测试点均通过，则视为该小题通过。 提交的代码得分为通过的小题分数之和。 1. (11 分) $N = 1$。 2. (13 分) $N = 3$。 3. (29 分) $N \leq 10$。 4. (22 分) 所有 $5$ 行的 $N$ 个格子均为同色。 5. (25 分) 无额外约束。 **注意，小题 $4$ 中的“所有 $5$ 行的 $N$ 个格子均为同色”不要误读为“所有 $N$ 列的 $5$ 个格子均为同色”。** ### 样例解释 1 可以制作出以下 $3$ 种パ研军旗： - 全部格子涂为红色，此时需重新涂色的格子为 $(1, 1), (3, 1), (4, 1), (5, 1)$ 共 $4$ 个。 - 全部格子涂为蓝色，此时需重新涂色的格子为 $(2, 1), (3, 1), (4, 1)$ 共 $3$ 个。 - 全部格子涂为白色，此时需重新涂色的格子为 $(1, 1), (2, 1), (3, 1), (5, 1)$ 共 $4$ 个。 其中“全部格子涂为蓝色”最优，需要重新涂色 $3$ 个格子。 顺便说一句，这属于 $N = 1$，满足小题 $1$ 的约束。 ### 样例解释 2 将第 $1$ 列涂为蓝色，第 $2$ 列涂为白色，第 $3$ 列涂为红色时，最少需要重新涂色 $10$ 个格子，且这是最优解。  （此处“★”表示被重新涂色的格子） 顺便说一句，这属于 $N = 3$，满足小题 $2$ 的约束。 ### 样例解释 3 如下图所示进行涂色最优，需要重新涂色 $28$ 个格子。（此处“★”表示被重新涂色的格子）  ### 样例解释 4 如下图所示进行涂色最优，需要重新涂色 $21$ 个格子。（此处“★”表示被重新涂色的格子）  由 ChatGPT 4.1 翻译