AT_pakencamp_2019_day3_d パ研軍旗

[problemUrl]: https://atcoder.jp/contests/pakencamp-2019-day3/tasks/pakencamp_2019_day3_d 筑駒パ研は，近い将来，パ研戦争に臨むことになりました．そのために，軍旗を作ることになりました． 旗のデザインは縦に $ 5 $ 個，横に $ N $ 個に分かれた $ 5\ \times\ N $ のマス目で表されます．上から $ i $ 行目，左から $ j $ 列目のマスを，$ (i,\ j) $ で表すことにします． 現在，旗のそれぞれのマスは赤・青・白・黒のいずれかで塗られています．より具体的には，マス $ (i,\ j) $ は色 $ S_{i,\ j} $ で塗られています．ただし，$ S_{i,\ j} $ は `R`, `B`, `W`, `#` のいずれかで，それぞれ赤・青・白・黒で塗られていることを表しています． E869120 君は，パ研軍旗を、次の条件を満たすように青・白・赤で塗り替えたいです． - $ N $ 個の列すべてにおいて，その列の $ 5 $ マスが「全部青」「全部白」「全部赤」のいずれかである - どの隣り合った $ 2 $ つの列も，色が異なる ただし，黒いマスがあったら条件を満たさないことに注意してください． 以下が，条件を満たす旗と条件を満たさない旗の例です．  - 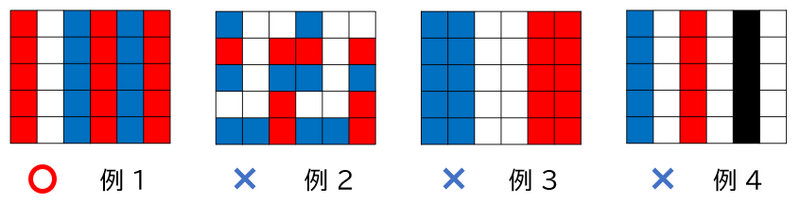例 $ 1 $ は条件を満たします． - 例 $ 2 $ は，例えば左から $ 2 $ 番目の列で青と白のマスがあり，$ 5 $ つ全部同じになっている必要があるという条件を満たしません． - 例 $ 3 $ は，例えば左から $ 3 $ 番目の列と左から $ 4 $ 番目の列の色が同じなので，条件を満たしません． - 例 $ 4 $ は，例えば左から $ 5 $ 番目の色が黒になっているので，条件を満たしません． E869120 君は，旗の作成時間を短くするため，できるだけ塗り替えるマスの個数を少なくしたいです． 最小でいくつのマスを塗り替える必要があるか求めるプログラムを書いてください．

入力は以下の形式で標準入力から与えられます． ただし、旗のそれぞれの行の色の情報 $ S_{i,\ 1},\ S_{i,\ 2},\ S_{i,\ 3},\ \dots,\ S_{i,\ N} $ は，これがつながった $ N $ 文字の文字列として入力されることに注意してください． > $ N $ $ S_{1,\ 1}\ S_{1,\ 2}\ S_{1,\ 3}\ \cdots\ S_{1,\ N} $ $ S_{2,\ 1}\ S_{2,\ 2}\ S_{2,\ 3}\ \cdots\ S_{2,\ N} $ $ S_{3,\ 1}\ S_{3,\ 2}\ S_{3,\ 3}\ \cdots\ S_{3,\ N} $ $ S_{4,\ 1}\ S_{4,\ 2}\ S_{4,\ 3}\ \cdots\ S_{4,\ N} $ $ S_{5,\ 1}\ S_{5,\ 2}\ S_{5,\ 3}\ \cdots\ S_{5,\ N} $

パ研軍旗を作るときに塗り替える必要のあるマスの個数の最小値を，$ 1 $ 行で出力してください．

### 制約 すべての入力データは，以下の制約を満たす． - $ N $ は $ 1\ \leq\ N\ \leq\ 999 $ をみたす整数 - $ S_{i,\ j} $ は `R`, `B`, `W`, `#` のいずれか ### 部分点 この問題はいくつかの小課題に分けられ，その小課題のすべてのテストケースに正解した場合に「この小課題に正解した」とみなされます． 提出したソースコードの得点は，正解した小課題の点数の合計となります． 1. (11 点) $ N\ =\ 1 $ である． 2. (13 点) $ N\ =\ 3 $ である． 3. (29 点) $ N\ \leq\ 10 $ である． 4. (22 点) $ 5 $ つの行すべてにおいて，その行の $ N $ 個のマスがすべて同じ色である． 5. (25 点) 追加の制約はない． **ただし，小課題 $ 4 $ について，「$ N $ 個の列すべてにおいて，その列の $ 5 $ 個のマスがすべて同じ色である」のような読み間違えをしないように注意してください．** ### Sample Explanation 1 以下の $ 3 $ 通りのパ研軍旗を作ることができます． - すべてのマスを赤にする．そのとき，マス $ (1,\ 1),\ (3,\ 1),\ (4,\ 1),\ (5,\ 1) $ の $ 4 $ マスを塗り替える必要がある． - すべてのマスを青にする．そのとき，マス $ (2,\ 1),\ (3,\ 1),\ (4,\ 1) $ の $ 3 $ マスを塗り替える必要がある． - すべてのマスを白にする．そのとき，マス $ (1,\ 1),\ (2,\ 1),\ (3,\ 1),\ (5,\ 1) $ の $ 4 $ マスを塗り替える必要がある． その中では，「すべてのマスを青」にするのが最適です．そのとき，塗り替えるマスの個数は $ 3 $ 個になります． ちなみに，これは $ N\ =\ 1 $ なので，小課題 $ 1 $ の制約をみたします． ### Sample Explanation 2 $ 1 $ 列目を青、$ 2 $ 列目を白、$ 3 $ 列目を赤にすると，塗り替えるマスの個数を $ 10 $ 個にできて，これが最適です． !\[ \](https://img.atcoder.jp/pakencamp-2019-day3/7607c1554c09d7d875918ccf09d65f78.png) (ここでは，「★」は塗り替えられたマスを表します) ちなみに，これは $ N\ =\ 3 $ なので，小課題 $ 2 $ の制約をみたします． ### Sample Explanation 3 次の図のように塗り替えるのが最適です．塗り替えるマスの数は $ 28 $ 個となります．(ここでは，「★」は塗り替えられたマスを表します) !\[ \](https://img.atcoder.jp/pakencamp-2019-day3/a660d84b5614953bf2b4e7ee8342fabd.png) ### Sample Explanation 4 次の図のように塗り替えるのが最適です．塗り替えるマスの数は $ 21 $ 個となります．(ここでは，「★」は塗り替えられたマスを表します) !\[ \](https://img.atcoder.jp/pakencamp-2019-day3/cb86f987229c1ab46e30411860964c19.png)