AT_pakencamp_2019_day3_f クリスマス飾り2

[problemUrl]: https://atcoder.jp/contests/pakencamp-2019-day3/tasks/pakencamp_2019_day3_f AtCoder 王国で最も高いタワーである，「AtCoder Tower」には，クリスマスを迎えるため，一直線上に $ N $ 個のオーナメントが飾られています． オーナメントには $ N $ 種類の色があり，それぞれ色 $ 1 $，色 $ 2 $，色 $ 3 $，..., 色 $ N $ と番号づけられています．最初，「AtCoder Tower」の，左から $ i $ 番目のオーナメントは，色 $ A_i $ です． さて，国王である高橋君は，いくつかのオーナメントを選び，取り除くことによって，飾り付けを「見栄えが良い」状態にしたいと考えています．「見栄えが良い」状態というのは，以下の条件を**すべて**満たすことを指します． - 残されたオーナメントの色の種類数が，$ 2 $ 色以下である． - 隣り合うオーナメントの色が同じであるような場所は存在しない． 例えば，\[A\] \[B\] のような取り除き方をすると，「見栄えが良い」状態となります．  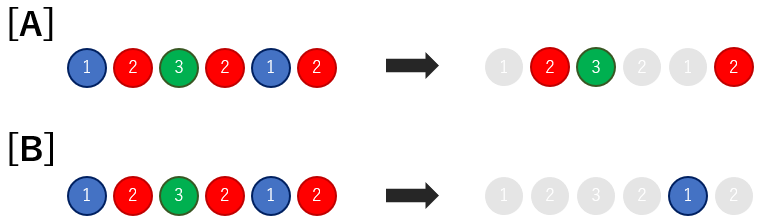一方で，\[C\] \[D\] のような取り除き方をすると，「見栄えが良い」状態にはなりません．  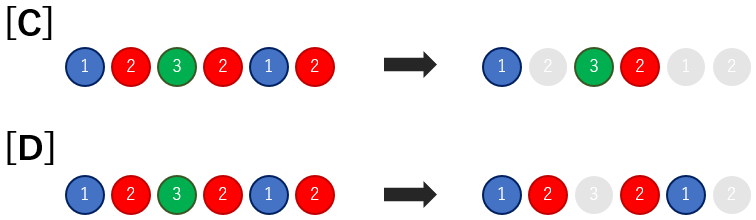ところで，「AtCoder Tower」では，クリスマスを迎えるための飾りつけが $ Q+1 $ 日間に渡って行われます．$ i $ 日目の夜には，左から $ X_i $ 番目のオーナメントの色が，色 $ Y_i $ に変更されます． そこで，$ i\ =\ 1,\ 2,\ ...\ Q+1 $ それぞれについて，以下の答えを求めてください． - もし高橋君が，$ i $ 日目の昼の段階で，飾りつけを「見栄えが良い」状態にする場合，最小で何個のオーナメントを取り除く必要があるでしょうか．

入力は以下の形式で標準入力から与えられます． > $ N $ $ A_1 $ $ A_2 $ $ A_3 $ ... $ A_N $ $ Q $ $ X_1 $ $ Y_1 $ $ X_2 $ $ Y_2 $ $ X_3 $ $ Y_3 $ : $ X_Q $ $ Y_Q $

$ Q+1 $ 行に渡って出力してください． $ i $ 行目には，$ i $ 日目の昼の時点で飾りつけを「見栄えの良い」状態にするために，最小で何個のオーナメントを取り除く必要があるか，出力してください．

### 制約 - $ 1\ \leq\ N\ \leq\ 3\ 000 $ - $ 0\ \leq\ Q\ \leq\ 7\ 000 $ - $ 1\ \leq\ X_i\ \leq\ N $ - $ 1\ \leq\ Y_i\ \leq\ N $ - $ 1\ \leq\ A_i\ \leq\ N $ - 入力はすべて整数 ### 部分点 この問題はいくつかの小課題に分けられ，その小課題のすべてのテストケースに正解した場合に「この小課題に正解した」とみなされます． 提出したソースコードの得点は，正解した小課題の点数の合計となります． 1. (2 点) $ N\ =\ 1 $，$ Q\ =\ 0 $． 2. (11 点) $ N\ \leq\ 15 $，$ Q\ =\ 0 $． 3. (12 点) $ A_i\ \leq\ 2 $，$ Y_i\ \leq\ 2 $． 4. (13 点) $ N\ \leq\ 250 $，$ Q\ =\ 0 $． 5. (18 点) $ Q\ =\ 0 $． 6. (44 点) 追加の制約はない． ただし，小課題6に関しては，以下のように採点されます． - $ Q\ \leq\ 600 $ を満たすテストケースすべてに正解すると，$ 24 $ 点が与えられる． - $ Q\ \leq\ 1\ 500 $ を満たすテストケースすべてに正解すると，さらに$ 5 $ 点が与えられる． - $ Q\ \leq\ 2\ 500 $ を満たすテストケースすべてに正解すると，さらに$ 5 $ 点が与えられる． - $ Q\ \leq\ 4\ 500 $ を満たすテストケースすべてに正解すると，さらに$ 5 $ 点が与えられる． - すべてのテストケースに正解すると，さらに$ 5 $ 点が与えられる． ### 小課題3のヒント この小課題は，どの日においても，オーナメントの色が色 $ 1 $ と色 $ 2 $ しかありません．つまり，「見栄えの良い」状態において，残されたオーナメントを左から見たとき，色 $ 1,\ 2,\ 1,\ ... $ と交互に並んでいるか，色 $ 2,\ 1,\ 2,\ ... $ と交互に並んでいるかのどちらかしかありません．小課題 3 に取り掛かる人は，このヒントを踏まえて考えてみるのも良いでしょう． ### Sample Explanation 1 この入力例において，オーナメントを取り除かなくても，飾りつけは「見栄えの良い状態」です． よって，$ 0 $ と出力するのが正解となります． ### Sample Explanation 2 以下の図のように，$ 4 $ つのオーナメントを取り除くと，「見栄えの良い」状態となります． !\[ \](https://img.atcoder.jp/pakencamp-2019-day3/14d4fc3b6f9bee0f55337ca3d11102a2.png) なお，この入力例は，小課題2の制約を満たします． ### Sample Explanation 3 $ Q=10 $ ですので，$ 11 $ 行に渡って出力しなければなりません．