AT_pakencamp_2019_day3_h パ研王国を守れ！

[problemUrl]: https://atcoder.jp/contests/pakencamp-2019-day3/tasks/pakencamp_2019_day3_h ついにパ研戦争が始まりました！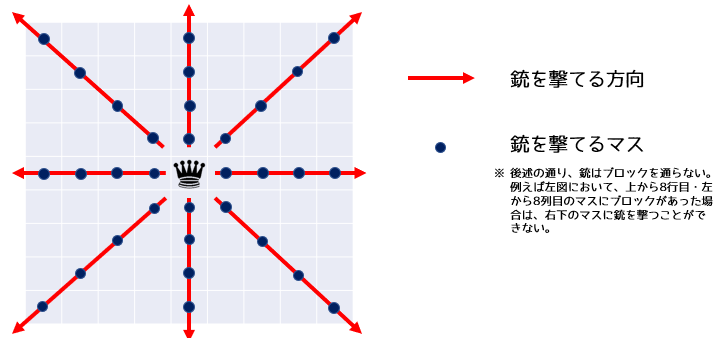 パ研戦争の戦場は，$ N\ \times\ N $ のマス目で表されます．この戦場の，上から $ i $ 番目，左から $ j $ 番目のマスを $ (i,\ j) $ で表すことにします． ここに，パ研王国の兵士が $ M $ 人，敵国の兵士が $ M $ 人立っています．より具体的には，$ S_{i,\ j} $ が `X` のときマス $ (i,\ j) $ にはパ研王国の兵士が立っており，`Q` のとき敵国の兵士が立っています．`.` のときは何もないマスです． 敵国の兵士は，銃を上下左右斜めの $ 8 $ 方向に撃つことができます．(具体的には，下図のようになっています)  敵国の兵士がパ研王国の兵士を直接撃てる状況にしないために，銃を通さないブロックをいくつかのマスに設置することにしました．ブロックを置ける条件は以下の通りです． - パ研王国の兵士も敵国の兵士もいない，何もないマスであること． できるだけ少ない数のブロックで，どの敵国の兵士もパ研王国の兵士を直接撃つことができないようにする方法を $ 1 $ つ求めてください． ただし，置いたブロックの個数に応じてこの問題の得点が決まるので，ブロックの個数を完全に最小化する必要はないことに注意してください．

入力は以下の形式で標準入力から与えられます． > $ N $ $ M $ $ S_{1,\ 1}\ S_{1,\ 2}\ S_{1,\ 3}\ \cdots\ S_{1,\ N} $ $ S_{2,\ 1}\ S_{2,\ 2}\ S_{2,\ 3}\ \cdots\ S_{2,\ N} $ $ S_{3,\ 1}\ S_{3,\ 2}\ S_{3,\ 3}\ \cdots\ S_{3,\ N} $ : : : $ S_{N,\ 1}\ S_{N,\ 2}\ S_{N,\ 3}\ \cdots\ S_{N,\ N} $

マス $ (i,\ j) $ の状態 $ V_{i,\ j} $ を，次のような文字とします． - マス $ (i,\ j) $ にブロックが置かれない場合，$ V_{i,\ j}\ =\ S_{i,\ j} $ - マス $ (i,\ j) $ にブロックが置かれる場合，$ V_{i,\ j}\ = $ `#` このとき，次のような形式で答えを出力してください． > $ V_{1,\ 1}\ V_{1,\ 2}\ V_{1,\ 3}\ \cdots\ V_{1,\ N} $ $ V_{2,\ 1}\ V_{2,\ 2}\ V_{2,\ 3}\ \cdots\ V_{2,\ N} $ $ V_{3,\ 1}\ V_{3,\ 2}\ V_{3,\ 3}\ \cdots\ V_{3,\ N} $ : : : $ V_{N,\ 1}\ V_{N,\ 2}\ V_{N,\ 3}\ \cdots\ V_{N,\ N} $

### 制約 すべての入力データは，以下の制約を満たします． - $ N\ =\ 100 $ - $ M\ =\ 300 $ - $ S_{i,\ j} $ は `Q`，`X`，`.` のいずれか - $ S_{i,\ j} $ が `Q` となるマスは，ちょうど $ M $ 個 - $ S_{i,\ j} $ が `X` となるマスは，ちょうど $ M $ 個 ### テストケース生成について パ研王国の兵士と敵国の兵士の位置は，「パ研王国の兵士と敵国の兵士が上下左右斜めに隣り合うことはない」という条件を満たす中でほぼランダムに生成されます．具体的には、[こちら](https://img.atcoder.jp/pakencamp-2019-day3/0c92256d19fa24d950ffeb3756ba9876.zip) の生成コードを元に作られております． ### 得点 提出に対する得点は，以下のように決定されます． - 採点に使われる $ 20 $ 個のテストケースのうち，$ 1 $ つでも条件を満たさない出力（不正なフォーマット・敵国の兵士がパ研王国の兵士を直接撃てるような出力）があれば，$ 0 $ 点となります． - そうでない場合，$ i $ 個目のテストケースの得点を $ a_i $ 点とするとき，提出に対する得点は $ floor(\frac{a_{1}+a_{2}+a_{3}+...+a_{20}}{20}) $ 点となります． 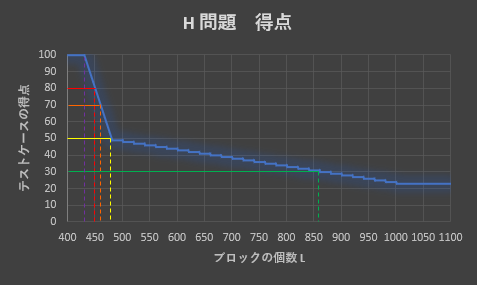なお，各テストケースに対する得点は，置いたブロックの個数を $ L $ とするとき，以下のように定められます． - $ 2\ 401\ \leq\ L $ のとき，$ 5 $ 点． - $ 1\ 901\ \leq\ L\ \leq\ 2\ 400 $ のとき，$ 14 $ 点． - $ 1\ 501\ \leq\ L\ \leq\ 1\ 900 $ のとき，$ 17 $ 点． - $ 1\ 201\ \leq\ L\ \leq\ 1\ 500 $ のとき，$ 20 $ 点． - $ 1\ 001\ \leq\ L\ \leq\ 1\ 200 $ のとき，$ 23 $ 点． - $ 481\ \leq\ L\ \leq\ 1\ 000 $ のとき，$ 50\ -\ (L\ -\ 480)\ \times\ 0.05 $ 点． - $ 431\ \leq\ L\ \leq\ 480 $ のとき，$ 100\ -\ (L\ -\ 430)\ \times\ 1 $ 点． - $ L\ \leq\ 430 $ のとき，$ 100 $ 点．  ### 入出力例 例えば，以下の入力例を考えましょう．（$ N,\ M $ が制約の条件を満たさないため，採点に用いられるデータには含まれません．） ``` 7 3 .Q..... ....X.. ....... .X....Q ....... Q.....X ....... 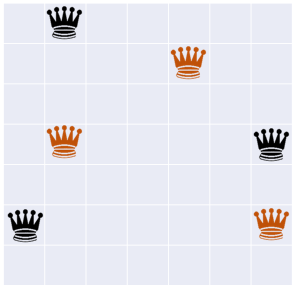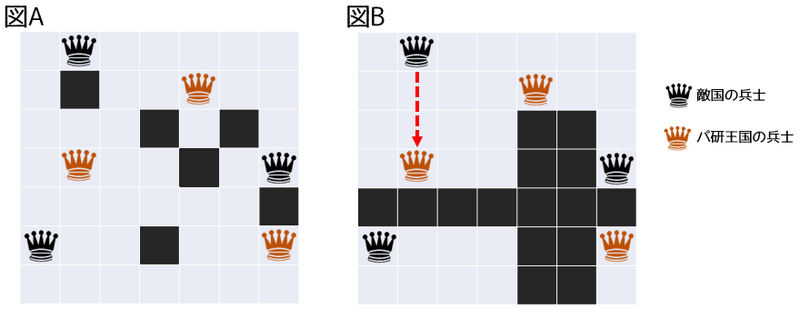``` この入力例において，ブロックを考えないとき，戦場は以下のようになります．  さて，以下の出力をすると，正解となります．この場合に置いたブロックの個数 $ L\ =\ 6 $ となります．（図A に対応します‥） ``` .Q..... .#..X.. ...#.#. .X..#.Q ......# Q..#..X ....... ``` また，以下の出力をすると，不正解となります．マス $ (1,\ 2) $ にいる敵国の兵士が，マス $ (4,\ 2) $ にいるパ研王国の兵士を撃つことができるからです． ``` .Q..... ....X.. ....##. .X..##Q ####### Q...##X ....##. ```  なお，この入力例は，$ N\ =\ 100 $，$ M\ =\ 300 $ の条件を満たさないため，テストデータには含まれません． 採点に用いられるすべてのテストケースは，$ N\ =\ 100 $，$ M\ =\ 300 $ を満たします．