AT_pakencamp_2023_day1_o Longest Bracket Subsequence

$ N $ 頂点の根付き木が与えられます。頂点には $ 1, 2, \ldots, N $ の番号が付いており、木の根は頂点 $ 1 $ です。 $ i $ $ (1 \le i \le N-1) $ 番目の辺は頂点 $ A_i $ と頂点 $ B_i $ をつないでいます。また、各頂点 $ i $ には文字 $ C_i $ $ (1 \le i \le N) $ が書き込まれています。 $ C_i $ は `(` か `)` のいずれかです。 以下の $ 3 $ 種類のクエリが $ Q $ 個与えられるので、順に処理してください。 $ j $ 個目のクエリは以下の通りです。 - $ T_j=1 $ のとき : 頂点 $ X_j $ に書かれている文字を $ Y_j $ に変更する - $ T_j=2 $ のとき : 頂点 $ S_j $ を根とする部分木の各頂点について、書かれている文字が `(` ならば `)` に、 `)` ならば `(` に変更する - $ T_j=3 $ のとき : 頂点 $ U_j $ から頂点 $ V_j $ へのパス上の頂点(両端含む)に書かれた文字を順に並べた文字列の(連続とは限らない)部分列のうち、正規括弧列であるものの長さの最大値を出力する。特に、空文字列は常に部分列かつ正規括弧列なので、最大値が必ず存在します。 (連続とは限らない)部分列とは？ 列から $ 0 $ 個以上の要素を削除し、残った要素を元の順序を保ったまま連結してできる列のことを指します。 例えば `((` や `)()` や空文字列は `)(()` の部分列ですが、 `(())` や `)))` は `)(()` の部分列ではありません。 正規括弧列とは？ `(` と `)` からなる文字列のうち、以下のいずれかを満たす物を指します。 - 空文字列である - ある正規括弧列 $ A $ が存在して、 `(` $ , A, $ `)` をこの順に連結して得られる - ある正規括弧列 $ A, B $ が存在して、 $ A, B $ をこの順に連結して得られる 例えば `(())()` や空文字列は正規括弧列ですが、 `())` や `)((` は正規括弧列ではありません。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ $ \vdots $ $ A_{N-1} $ $ B_{N-1} $ $ C_1 $ $ C_2 $ $ \ldots $ $ C_N $ $ Q $ $ \mathrm{query}_1 $ $ \mathrm{query}_2 $ $ \vdots $ $ \mathrm{query}_Q $ ここで、各クエリ $ \mathrm{query}_i $ は以下のいずれかの形式で与えられる。 > $ 1 $ $ X_i $ $ Y_i $ > $ 2 $ $ S_i $ > $ 3 $ $ U_i $ $ V_i $

$ T_j=3 $ のクエリに対する答えを順に出力せよ。

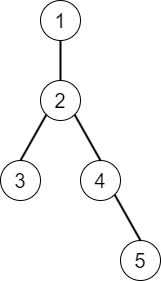
### Sample Explanation 1 木は以下のようになっています。  それぞれのクエリは次のように処理されます。 1. パス上の頂点は $ (1, 2, 4, 5) $ であり、頂点に書かれた文字を連結すると `(())` になります。これは正規括弧列なので、長さ $ 4 $ を出力します。 2. パス上の頂点は $ (3, 2, 4) $ であり、頂点に書かれた文字を連結すると `)()` になります。この部分列で最長の正規括弧列は `()` なので、長さ $ 2 $ を出力します。 3. 頂点 $ 2 $ の部分木の頂点 $ 2, 3, 4, 5 $ に書かれた文字が変更され、頂点 $ 1, 2, 3, 4, 5 $ に書かれた文字はそれぞれ `(`, `)`, `(`, `(`, `(` になります。 4. パス上の頂点は $ (5, 4, 2, 1) $ であり、頂点に書かれた文字を連結すると `(()(` になります。この部分列で最長の正規括弧列は `()` なので、長さ $ 2 $ を出力します。 ### Constraints - $ 1 \leq N, Q\leq 2\times 10^5 $ - $ 1 \le A_i < B_i \le N $ $ (1 \leq i \leq N-1) $ - $ C_i= $ `(` または $ C_i= $ `)` $ (1 \leq i \leq N) $ - $ 1 \leq T_j \leq 3 $ $ (1 \leq j \leq Q) $ - $ T_j=1 $ のとき、 $ 1 \le X_j \le N $ かつ $ Y_j= $ `(` または $ Y_j= $ `)` $ (1 \leq j \leq Q) $ - $ T_j=2 $ のとき、 $ 1 \le S_j \le N $ $ (1 \leq j \leq Q) $ - $ T_j=3 $ のとき、 $ 1 \le U_j, V_j \le N $ $ (1 \leq j \leq Q) $ - 入力は全て、整数か `(` か `)` のいずれか