AT_pakencamp_2023_day1_o Longest Bracket Subsequence

给定一棵有 $N$ 个顶点的有根树。顶点编号为 $1, 2, \ldots, N$，树的根为顶点 $1$。第 $i$ 条边 $(1 \leq i \leq N-1)$ 连接顶点 $A_i$ 和顶点 $B_i$。每个顶点 $i$ $(1 \leq i \leq N)$ 上写有一个字符 $C_i$，其中 $C_i$ 只能是 `(` 或 `)`。 有 $Q$ 个操作，需要按顺序处理。第 $j$ 个操作有三种类型： - 当 $T_j=1$ 时：将顶点 $X_j$ 上的字符修改为 $Y_j$。 - 当 $T_j=2$ 时：将以顶点 $S_j$ 为根的子树中所有顶点上的字符取反，即 `(` 变为 `)`，`)` 变为 `(`。 - 当 $T_j=3$ 时：输出从顶点 $U_j$ 到顶点 $V_j$ 的路径上（包括两端）所有顶点上的字符依次连接得到的字符串，在其所有（不一定连续的）子序列中，最长的“正规括号序列”的长度。特别地，空串总是子序列也是正规括号序列，所以最大值一定存在。 什么是不连续子序列？它指的是从原序列中删除 $0$ 个或多个元素，保留剩余元素原本的顺序后连成的序列。例如，`((`、`)()` 和空串都是 `)(()` 的子序列，而 `(())` 和 `)))` 则不是。 什么是正规括号序列？正规括号序列是只由 `(` 和 `)` 构成的字符串，满足下列之一： - 是空串； - 存在一个正规括号序列 $A$，将 `(`、$A$、`)` 按顺序连接得到； - 存在两个正规括号序列 $A$、$B$，按顺序连接 $A$ 和 $B$ 得到结果。 例如，`(())()` 和空串都是正规括号序列，但 `())` 和 `)((` 不是。

输入按以下格式从标准输入读入。 > $N$ > $A_1$ $B_1$ > $A_2$ $B_2$ > ⋮ > $A_{N-1}$ $B_{N-1}$ > $C_1$ $C_2$ ⋯ $C_N$ > $Q$ > $\mathrm{query}_1$ > $\mathrm{query}_2$ > ⋮ > $\mathrm{query}_Q$ 其中，每个操作 $\mathrm{query}_i$ 有以下三种形式之一： > $1$ $X_i$ $Y_i$ > $2$ $S_i$ > $3$ $U_i$ $V_i$

对于每个 $T_j=3$ 的操作，请顺序输出答案。

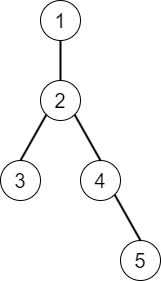
### 样例解释 1 这棵树结构如下所示。  每个操作的处理如下： 1. 路径上的顶点为 $1,2,4,5$，它们上的字符依次连接得到 `(()))`。这是一个正规括号序列，因此输出长度 $4$。 2. 路径上的顶点为 $3,2,4$，它们上的字符依次连接得到 `)()`。其最长的正规括号子序列为 `()`，长度为 $2$。 3. 将以顶点 $2$ 为根的子树中顶点 $2,3,4,5$ 上的字符全部取反，结果顶点 $1,2,3,4,5$ 上的字符依次为 `(`,`)`,`(`,`(`,`(`。 4. 路径上的顶点为 $5,4,2,1$，它们上的字符依次连接得到 `(()(`。其最长的正规括号子序列为 `()`，长度为 $2$。 ### 数据范围 - $1 \leq N, Q \leq 2 \times 10^5$ - $1 \leq A_i < B_i \leq N$ $(1 \leq i \leq N-1)$ - $C_i$ 为 `(` 或 `)` $(1 \leq i \leq N)$ - $1 \leq T_j \leq 3$ $(1 \leq j \leq Q)$ - 当 $T_j=1$ 时，$1 \leq X_j \leq N$ 且 $Y_j$ 为 `(` 或 `)` $(1 \leq j \leq Q)$ - 当 $T_j=2$ 时，$1 \leq S_j \leq N$ $(1 \leq j \leq Q)$ - 当 $T_j=3$ 时，$1 \leq U_j, V_j \leq N$ $(1 \leq j \leq Q)$ - 输入只包含整数或 `(` 或 `)` 由 ChatGPT 5 翻译