AT_pakencamp_2024_day1_l Taxi of Paken Kingdom

パ研王国には $ N $ 個の町 $ 1, 2, \ldots, N $ と、異なる $ 2 $ つの町を双方向に繋ぐ $ M $ 個の道路 $ 1, 2, \ldots, M $ があります。道路 $ i $ $ (1 \leq i \leq M) $ は町 $ A_i $ と町 $ B_i $ を双方向に繋いでおり、 $ 2 $ つの異なる道路が同じ町の組を結ぶことはありません。どの町からどの町へも $ 0 $ 本以上の道路を通り移動できますが、道路以外を通って町から町へ移動することはできません。 さて、今年もパ研合宿の季節がやってきました。パ研合宿は町 $ 1 $ で開催されるため、全ての町から参加者が町 $ 1 $ に移動します。荷物を持って移動するのは大変なので、参加者はタクシーを使って町を移動することになりました。 パ研王国には $ N $ 個のタクシー会社 $ 1, 2, \ldots, N $ があり、それぞれの会社には以下のような規則があります。 - タクシー会社 $ i $ のタクシーには、町 $ i $ からのみ乗車できる。 - タクシー会社 $ i $ のタクシーの運賃は、移動した距離によらず $ C_i $ である。 - タクシー会社 $ i $ のタクシーは、乗車してから最大 $ R_i $ 本の道路しか通ることができない。 複数のタクシーを乗り継ぐこともできますが、タクシー以外の手段で町を移動してはいけません。 参加者のために、それぞれの町からタクシーのみを用いて町 $ 1 $ に移動するために必要な運賃の合計の最小値を求めてください。なお、この制約下で全ての町からタクシーのみを用いて町 $ 1 $ に移動できることが証明できます。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ M $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ $ \vdots $ $ A_M $ $ B_M $ $ C_1 $ $ C_2 $ $ \ldots $ $ C_N $ $ R_1 $ $ R_2 $ $ \ldots $ $ R_N $

$ N $ 行出力せよ。 $ i $ 行目 $ (1 \leq i \leq N) $ には、町 $ i $ から町 $ 1 $ にタクシーのみを用いて移動するのに必要な運賃の合計の最小値を出力せよ。

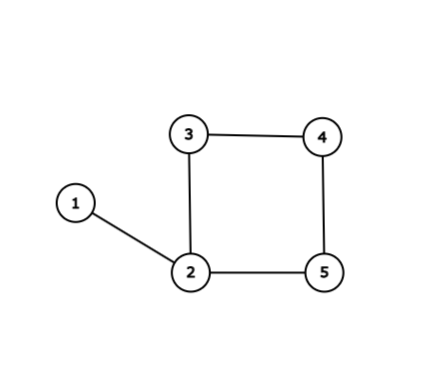
### Sample Explanation 1 パ研王国は以下のようになります。  例えば、町 $ 5 $ から町 $ 1 $ へは以下のように移動できます。 1. 町 $ 5 $ でタクシー会社 $ 5 $ のタクシーに乗り、町 $ 4 $ まで移動する。 2. 町 $ 4 $ でタクシー会社 $ 4 $ のタクシーに乗り、町 $ 1 $ まで移動する。 このときに必要な運賃の合計は $ 100+200=300 $ です。運賃の合計が $ 300 $ 未満となる移動方法はないため、 $ 300 $ を出力します。 ### Constraints - $ 2 \leq N \leq 2 \times 10^5 $ - $ 1 \leq M \leq 2 \times 10^5 $ - $ 1 \leq A_i < B_i \leq N $ ( $ 1 \leq i \leq M $ ) - $ (A_i, B_i) \neq (A_j, B_j) $ ( $ 1 \leq i < j \leq M $ ) - どの町からどの町へも $ 0 $ 本以上の道路を通り移動できる - $ 1 \leq C_i \leq 10^9 $ ( $ 1 \leq i \leq N $ ) - $ 1 \leq R_i \leq $ $ 10 $ ( $ 1 \leq i \leq N $ ) - 入力は全て整数